题目内容
19.求直线y=2x-1与两坐标轴围成三角形的面积.分析 根据一次函数的性质,求得函数y=2x-1的图象与两条坐标轴交点分别是(0,-1)和(-$\frac{1}{2}$,0),所围成的三角形是直角三角形,利用三角形面积公式,求得三角形的面积.
解答 解:根据一次函数的性质,求得函数y=2x-1的图象与两条坐标轴交点分别是(0,-1)和(-$\frac{1}{2}$,0),
即高为1,底为$\frac{1}{2}$.
∴所围成的三角形的面积为:$\frac{1}{2}$×$1×\frac{1}{2}$=$\frac{1}{4}$.
点评 根据一次函数的性质,求得函数y=2x-1的图象与两条坐标轴交点,即为所求三角形的高和底,即可求出三角形的面积.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
8.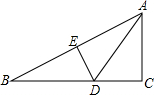 如图,△ABC中,∠ACB=90°,∠B=30°,DE垂直平分AB,若DE=1.5cm,则BC的长是( )
如图,△ABC中,∠ACB=90°,∠B=30°,DE垂直平分AB,若DE=1.5cm,则BC的长是( )
 如图,△ABC中,∠ACB=90°,∠B=30°,DE垂直平分AB,若DE=1.5cm,则BC的长是( )
如图,△ABC中,∠ACB=90°,∠B=30°,DE垂直平分AB,若DE=1.5cm,则BC的长是( )| A. | 3cm | B. | 4.5cm | C. | 6cm | D. | 7.5cm |
 如图,△ABC和△AED为等腰三角形,AB=AC,AD=AE,且∠BAC=∠DAE.连接BE、CD交于点O,连接AO并延长交CE为点H.
如图,△ABC和△AED为等腰三角形,AB=AC,AD=AE,且∠BAC=∠DAE.连接BE、CD交于点O,连接AO并延长交CE为点H. 如图,有三个村庄分别是A、B、C,现计划修建一个居民活动中心P,要求到三个村庄的距离相等,请在图中确定活动中心P的位置.
如图,有三个村庄分别是A、B、C,现计划修建一个居民活动中心P,要求到三个村庄的距离相等,请在图中确定活动中心P的位置. 已知:如图,直线m∥n.Rt△ABC与直线m、n分别相交,且∠1=25°,∠2=80°,求∠A的度数.
已知:如图,直线m∥n.Rt△ABC与直线m、n分别相交,且∠1=25°,∠2=80°,求∠A的度数. 如图,在△ABC中,GD⊥AC于点D,∠AFE=∠ABC,∠1+∠2=180°,∠AEF=65°.求:∠1的度数.
如图,在△ABC中,GD⊥AC于点D,∠AFE=∠ABC,∠1+∠2=180°,∠AEF=65°.求:∠1的度数. 如图,已知梯形ABCD,AD∥BC,∠ABD=∠ACD.求证:AB=DC.
如图,已知梯形ABCD,AD∥BC,∠ABD=∠ACD.求证:AB=DC.