Question

14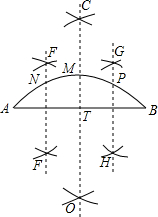．小明四等分弧AB，他的作法如下：
（1）连接AB（如图）；
（2）作AB的垂直平分线CD交弧AB于点M，交AB于点T；
（3）分别作AT，TB的垂直平分线EF，GH，交弧AB于N，P两点，则N，M，P三点把弧AB四等分．
你认为小明的作法是否正确：不正确，理由是弦AN与MN不相等，则$\widehat{AN}$≠$\widehat{MN}$．

Answer 1

分析 由作法可知，弦AN与MN不相等，根据圆心角、弧、弦的关系定理得到$\widehat{AN}$≠$\widehat{MN}$，由此得出小明的作法不正确．

解答 解：小明的作法不正确．理由是：
如图，连结AN并延长，交CD于J，连结MN，设EF与AB交于I．
由作法可知，EF∥CD，AI=IT，
∴AN=NJ，
∵∠NMJ＞∠NJM，
∴NJ＞MN，
∴AN＞MN，
∴弦AN与MN不相等，
则$\widehat{AN}$≠$\widehat{MN}$．
故答案为不正确；弦AN与MN不相等，则$\widehat{AN}$≠$\widehat{MN}$．

点评 本题考查了作图-复杂作图，线段垂直平分线的性质，圆心角、弧、弦的关系定理．根据作法得出弦AN与MN不相等或弦BP与PM不相等是解题的关键．