题目内容
15．
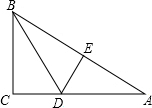如图，在Rt△ABC中，∠C=90°，把AB对折后，点A与点B重合，折痕为DE．（1）若∠A=25°，求∠BDC的度数；
（2）若AC=4，BC=2，求BD．
分析 （1）由翻折的性质可知∠A=∠DBA=25°，由三角形外角的性质可知∠CBD=50°；
（2）设BD=x，由翻折的性质可知DA=x，从而求得CD=4-x，最后在△BCD中由勾股定理可求得BD的长．
解答 解：（1）由翻折的性质：∠A=∠DBA=25°．
∠BDC=∠A+∠ABD=25°+25°=50°．
（2）设BD=x．
由翻折的性质可知DA=BD=x，则CD=4-x．
在Rt△BCD中，由勾股定理得；BD2=CD2+BC2，即x2=（4-x）2+22．
解得：x=2.5．即BD=2.5．
点评 本题主要考查的是翻折的性质，依据勾股定理列出关于x的方程是解题的关键．
练习册系列答案
赢在课堂名师课时计划系列答案
相关题目
6．在一个不透明的口袋中装有12个白球、16个黄球、24个红球、28个绿球，除颜色其余都相同，小明通过多次摸球实验后发现，摸到某种颜色的球的频率稳定在0.3左右，则小明做实验时所摸到的球的颜色是（ ）
| A． | 白色 | B． | 黄色 | C． | 红色 | D． | 绿色 |
20．
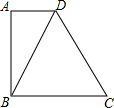如图所示，在四边形ABCD中，AB⊥BC，AB⊥AD，BD=BC，∠C=60°，如果△DBC的周长为m，则AD的长为（ ）
如图所示，在四边形ABCD中，AB⊥BC，AB⊥AD，BD=BC，∠C=60°，如果△DBC的周长为m，则AD的长为（ ）| A． | $\frac{m}{3}$ | B． | $\frac{m}{6}$ | C． | $\frac{m}{8}$ | D． | $\frac{m}{12}$ |
如图，有三个村庄分别是A、B、C，现计划修建一个居民活动中心P，要求到三个村庄的距离相等，请在图中确定活动中心P的位置．
如图，在△ABC中，GD⊥AC于点D，∠AFE=∠ABC，∠1+∠2=180°，∠AEF=65°．求：∠1的度数．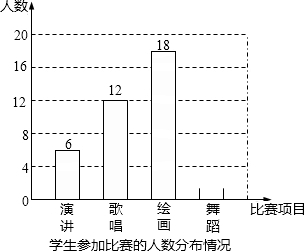
双城区某中学为了丰富校园文化生活，校学生会决定举办演讲、歌唱、绘画、舞蹈四项比赛，要求每位学生都参加．且只能参加一项比赛．围绕“你参赛的项目是什么？（只写一项）”的问题，校学生会在全校范围内随机抽取部分学生进行问卷调查．将调查问卷适当整理后绘制成如图所示的不完整的条形统计图．其中参加舞蹈比赛的人数与参加歌唱比赛的人数之比为1：3．请你根据以上信息回答下列问题：