题目内容
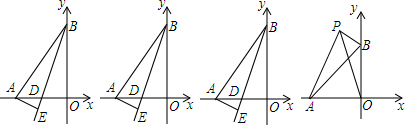
16. 如图,抛物线y=-$\frac{1}{2}$x2+$\frac{7}{2}$x与矩形OABC的边AB交于点D、B,A(0,3),C(6,0),则图中抛物线与矩形OABC形成的阴影部分的面积的和为( )
如图,抛物线y=-$\frac{1}{2}$x2+$\frac{7}{2}$x与矩形OABC的边AB交于点D、B,A(0,3),C(6,0),则图中抛物线与矩形OABC形成的阴影部分的面积的和为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 根据抛物线的对称性得到图中阴影部分的面积=矩形OADE的面积.
解答 解:作DE⊥OC于E,
根据抛物线的对称性得到:S阴影=S矩形OADE.
∵A(0,3),
∴D的纵坐标为3,
代入y=-$\frac{1}{2}$x2+$\frac{7}{2}$x得,3=-$\frac{1}{2}$x2+$\frac{7}{2}$x,
解得x=1或6,
∴AD=1,OA=3,
∴S阴影=S矩形OADE=1×3=3.
故选A.
点评 本题考查了二次函数的性质.利用抛物线的对称性质将所求的阴影部分的面积转化为规则图形的面积是解题的难点.

练习册系列答案
相关题目
6.在一个不透明的口袋中装有12个白球、16个黄球、24个红球、28个绿球,除颜色其余都相同,小明通过多次摸球实验后发现,摸到某种颜色的球的频率稳定在0.3左右,则小明做实验时所摸到的球的颜色是( )
| A. | 白色 | B. | 黄色 | C. | 红色 | D. | 绿色 |
8.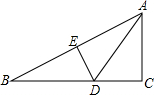 如图,△ABC中,∠ACB=90°,∠B=30°,DE垂直平分AB,若DE=1.5cm,则BC的长是( )
如图,△ABC中,∠ACB=90°,∠B=30°,DE垂直平分AB,若DE=1.5cm,则BC的长是( )
 如图,△ABC中,∠ACB=90°,∠B=30°,DE垂直平分AB,若DE=1.5cm,则BC的长是( )
如图,△ABC中,∠ACB=90°,∠B=30°,DE垂直平分AB,若DE=1.5cm,则BC的长是( )| A. | 3cm | B. | 4.5cm | C. | 6cm | D. | 7.5cm |
 如图,有三个村庄分别是A、B、C,现计划修建一个居民活动中心P,要求到三个村庄的距离相等,请在图中确定活动中心P的位置.
如图,有三个村庄分别是A、B、C,现计划修建一个居民活动中心P,要求到三个村庄的距离相等,请在图中确定活动中心P的位置. 如图,在△ABC中,GD⊥AC于点D,∠AFE=∠ABC,∠1+∠2=180°,∠AEF=65°.求:∠1的度数.
如图,在△ABC中,GD⊥AC于点D,∠AFE=∠ABC,∠1+∠2=180°,∠AEF=65°.求:∠1的度数. 如图,已知,线段AB=6,点C是AB的中点,点D是线段AC上的点,且DC=$\frac{1}{3}$AC,求线段BD的长.
如图,已知,线段AB=6,点C是AB的中点,点D是线段AC上的点,且DC=$\frac{1}{3}$AC,求线段BD的长.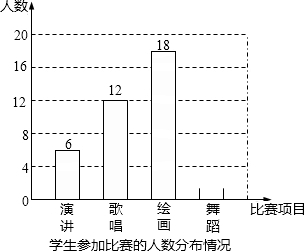 双城区某中学为了丰富校园文化生活,校学生会决定举办演讲、歌唱、绘画、舞蹈四项比赛,要求每位学生都参加.且只能参加一项比赛.围绕“你参赛的项目是什么?(只写一项)”的问题,校学生会在全校范围内随机抽取部分学生进行问卷调查.将调查问卷适当整理后绘制成如图所示的不完整的条形统计图.其中参加舞蹈比赛的人数与参加歌唱比赛的人数之比为1:3.请你根据以上信息回答下列问题:
双城区某中学为了丰富校园文化生活,校学生会决定举办演讲、歌唱、绘画、舞蹈四项比赛,要求每位学生都参加.且只能参加一项比赛.围绕“你参赛的项目是什么?(只写一项)”的问题,校学生会在全校范围内随机抽取部分学生进行问卷调查.将调查问卷适当整理后绘制成如图所示的不完整的条形统计图.其中参加舞蹈比赛的人数与参加歌唱比赛的人数之比为1:3.请你根据以上信息回答下列问题: