题目内容
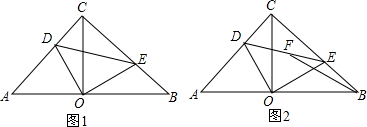
6. 如图,已知点A、C、E在同一直线上,△ABC和△CDE都是等边三角形,M、N分别为AD、BE的中点,求证:△CMN是等边三角形.
如图,已知点A、C、E在同一直线上,△ABC和△CDE都是等边三角形,M、N分别为AD、BE的中点,求证:△CMN是等边三角形.
分析 根据等腰三角形的性质得到∠BCA=∠DCE=60°,BC=AC,CD=CE,于是得到∠BCD=180°-∠BCA-∠DCE=60°,推出∠DCA=∠BCE,证得△ACD≌△BCE(SAS),根据全等三角形的性质得到∠ACD=∠BEC,AD=BE,由M,N分别为AD,BE的中点,得到DM=EN,推出△MDC≌△NEC(SAS),根据全等三角形的性质得到CM=CN∠DMC=∠NCE,求出∠MCN=60°,即可得到结论.
解答 证明:∵△ABC和△CDE为正三角形,
∴∠BCA=∠DCE=60°,BC=AC,CD=CE,
∴∠BCD=180°-∠BCA-∠DCE=60°,
∴∠BCD+∠DCE=∠BCD+∠BCA,
即∠DCA=∠BCE,
在△ACD和△BCE中,$\left\{\begin{array}{l}{AC=BC}\\{∠DCA=∠BCE}\\{EC=DC}\end{array}\right.$,
∴△ACD≌△BCE(SAS),
∴∠ACD=∠BEC,AD=BE,
∵M,N分别为AD,BE的中点,
∴DM=EN,
在△MDC和△NEC中 $\left\{\begin{array}{l}{DM=EN}\\{∠ACD=∠BEC}\\{DC=CE}\end{array}\right.$,
∴△MDC≌△NEC(SAS),
∴CM=CN∠DMC=∠NCE,
∵∠NCE+∠DCN=60°,
∴∠MCD+∠DCN=60°,
即∠MCN=60°,
在△MNC中,MC=NC,MCN=60°,
∴△CMN为正三角形.
点评 本题查看了全等三角形的判定和性质,等边三角形的性质,线段中点的定义,三角形的内角和定理,准确的找出全等三角形是解题的关键.

练习册系列答案
相关题目
15.请观察:13+23=9=(1+2)2,13+23+33=36=(1+2+3)2,那么13+23+33+43+53等于( )
| A. | 15 | B. | 115 | C. | 225 | D. | 625 |
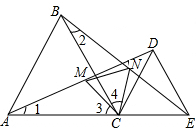
 如图,在△ABC中,GD⊥AC于点D,∠AFE=∠ABC,∠1+∠2=180°,∠AEF=65°.求:∠1的度数.
如图,在△ABC中,GD⊥AC于点D,∠AFE=∠ABC,∠1+∠2=180°,∠AEF=65°.求:∠1的度数.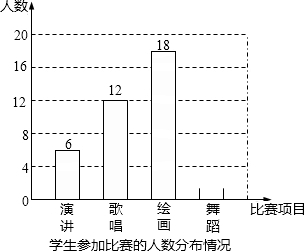 双城区某中学为了丰富校园文化生活,校学生会决定举办演讲、歌唱、绘画、舞蹈四项比赛,要求每位学生都参加.且只能参加一项比赛.围绕“你参赛的项目是什么?(只写一项)”的问题,校学生会在全校范围内随机抽取部分学生进行问卷调查.将调查问卷适当整理后绘制成如图所示的不完整的条形统计图.其中参加舞蹈比赛的人数与参加歌唱比赛的人数之比为1:3.请你根据以上信息回答下列问题:
双城区某中学为了丰富校园文化生活,校学生会决定举办演讲、歌唱、绘画、舞蹈四项比赛,要求每位学生都参加.且只能参加一项比赛.围绕“你参赛的项目是什么?(只写一项)”的问题,校学生会在全校范围内随机抽取部分学生进行问卷调查.将调查问卷适当整理后绘制成如图所示的不完整的条形统计图.其中参加舞蹈比赛的人数与参加歌唱比赛的人数之比为1:3.请你根据以上信息回答下列问题: 如图,已知梯形ABCD,AD∥BC,∠ABD=∠ACD.求证:AB=DC.
如图,已知梯形ABCD,AD∥BC,∠ABD=∠ACD.求证:AB=DC.