题目内容
20.以下列各组数为边长首尾相连,能构成直角三角形的一组是( )| A. | 2,3,4 | B. | 1,2,$\sqrt{3}$ | C. | 5,12,17 | D. | 6,8,12 |
分析 如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.
解答 解:根据22+32≠42,可知其不能构成直角三角形;
根据12+($\sqrt{3}$)2=22,可知其能构成直角三角形;
根据52+122≠172,可知其不能构成直角三角形;
根据62+82≠122,可知其不能构成直角三角形;
故选:B.
点评 本题主要考查了勾股定理的逆定理的运用,解题时注意:要判断一个角是不是直角,先要构造出三角形,然后知道三条边的大小,用较小的两条边的平方和与最大的边的平方比较,如果相等,则三角形为直角三角形;否则不是.

练习册系列答案
相关题目
8.求一个正数的立方根,有些数可以直接求得,如$\root{3}{8}$=2,有些数则不能直接求得,如$\root{3}{9}$,但可以利用计算器求得,还可以通过一组数的内在联系,运用规律求得,请同学观察下表:
已知$\root{3}{2.16}$≈1.293,$\root{3}{21.6}$≈2.785,$\root{3}{216}$≈6,运用你发现的规律求$\root{3}{21600000}$=278.5.
| n | 0.008 | 8 | 8000 | 8000000 | … |
| $\root{3}{n}$ | 0.2 | 2 | 20 | 200 | … |
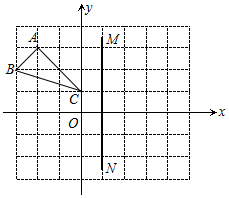 已知△ABC在平面直角坐标系中的位置如图所示,每个小正方形的边长为1,点ABC都在格点上,直线MN经过点(1,0)且垂直于x轴,若△A1B1C1和△ABC关于直线MN成轴对称
已知△ABC在平面直角坐标系中的位置如图所示,每个小正方形的边长为1,点ABC都在格点上,直线MN经过点(1,0)且垂直于x轴,若△A1B1C1和△ABC关于直线MN成轴对称 如图所示,三条射线OA、OB、OC交于一点O;则该图中共有3个角.
如图所示,三条射线OA、OB、OC交于一点O;则该图中共有3个角.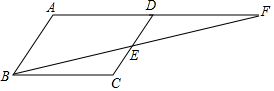 在?ABCD中,E为CD的中点,连接BE并延长交AD的延长线于F.求证:AD=DF.
在?ABCD中,E为CD的中点,连接BE并延长交AD的延长线于F.求证:AD=DF.