Question

9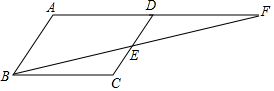．在?ABCD中，E为CD的中点，连接BE并延长交AD的延长线于F．求证：AD=DF．

Answer 1

分析 利用平行四边形的性质可证明△BEC≌△FED，则可证得BC=DF，结合平行四边形的性质可得AD=DF．

解答 证明：
∵四边形ABCD为平行四边形，
∴AD∥BC，AD=BC，
∴∠CBE=∠DFE，
∵E为CD的中点，
∴CE=DE，
在△BEC和△FED中
$\left\{\begin{array}{l}{∠CBE=∠DFE}\\{∠BEC=∠DEF}\\{CE=DE}\end{array}\right.$
∴△BEC≌△FED（AAS），
∴BC=DF，
∴AD=DF．

点评 本题主要考查平行四边形的性质和全等三角形的判定和性质，证得△BEC≌△FED是解题的关键．