题目内容
8.已知关于x的一元二次方程x2-(2k+1)x+k2+2k=0有两个实数根x1,x2,(1)求实数k的取值范围.
(2)是否存在实数k使得x1x2-x12-x22=-7成立?若存在,请求出k的值;若不存在,请说明理由.
分析 (1)根据判别式的意义得到△=(2k+1)2-4(k2+2k)≥0,然后解不等式即可;
(2)根据根与系数的关系得到x1+x2=2k+1,x1x2=k2+2k,再把x1x2-x12-x22=-7变形为-(x1+x2)2+3x1•x2=-7,所以-(2k+1)2+3(k2+2k)=-7,然后解方程后利用(1)中的范围确定满足条件的k的值.
解答 解:(1)根据题意得△=(2k+1)2-4(k2+2k)≥0,
解得k≤$\frac{1}{4}$;
(2)根据题意得x1+x2=2k+1,x1x2=k2+2k,
∵x1x2-x12-x22=-7.
∴x1x2-[(x1+x2)2-2x1x2]=-7,
即-(x1+x2)2+3x1•x2=-7
∴-(2k+1)2+3(k2+2k)=-7
整理得k2-2k-6=0,解得k1=1+$\sqrt{7}$(舍去),k2=1-$\sqrt{7}$
∴k=1-$\sqrt{7}$.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了根的判别式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.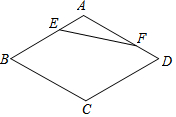 如图,在菱形ABCD中,∠B=60°,AB=a,点E,F分别是边AB,AD上的动点,且AE+AF=a,则线段EF的最小值为( )
如图,在菱形ABCD中,∠B=60°,AB=a,点E,F分别是边AB,AD上的动点,且AE+AF=a,则线段EF的最小值为( )
 如图,在菱形ABCD中,∠B=60°,AB=a,点E,F分别是边AB,AD上的动点,且AE+AF=a,则线段EF的最小值为( )
如图,在菱形ABCD中,∠B=60°,AB=a,点E,F分别是边AB,AD上的动点,且AE+AF=a,则线段EF的最小值为( )| A. | 2$\sqrt{3}$a | B. | $\frac{\sqrt{3}}{2}$a | C. | $\sqrt{3}$a | D. | $\frac{a}{2}$ |
 如图,平面直角坐标系xOy中,正方形一的顶点坐标分别为A(1,3),B(1,1),C(3,1),D(3,3).直线y=kx+b(k≠0)经过点P(-2,0),则$\frac{k}{b}$=$\frac{1}{2}$;若直线y=kx+b在绕点P旋转的过程中,同时与AB边、CD边有公共点,则b的取值范围是$\frac{2}{3}$<b<$\frac{6}{5}$.
如图,平面直角坐标系xOy中,正方形一的顶点坐标分别为A(1,3),B(1,1),C(3,1),D(3,3).直线y=kx+b(k≠0)经过点P(-2,0),则$\frac{k}{b}$=$\frac{1}{2}$;若直线y=kx+b在绕点P旋转的过程中,同时与AB边、CD边有公共点,则b的取值范围是$\frac{2}{3}$<b<$\frac{6}{5}$.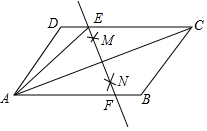 在平行四边形ABCD中,连接AC,按以下步骤作图,分别以A、C为圆心,以大于$\frac{1}{2}$AC的长为半径画弧,两弧分别相交于点M、N,作直线MN交CD于点E,交AB于点F.若AB=6,BC=4,则△ADE的周长为10.
在平行四边形ABCD中,连接AC,按以下步骤作图,分别以A、C为圆心,以大于$\frac{1}{2}$AC的长为半径画弧,两弧分别相交于点M、N,作直线MN交CD于点E,交AB于点F.若AB=6,BC=4,则△ADE的周长为10.