题目内容

17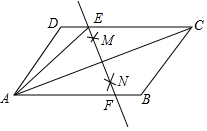．在平行四边形ABCD中，连接AC，按以下步骤作图，分别以A、C为圆心，以大于$\frac{1}{2}$AC的长为半径画弧，两弧分别相交于点M、N，作直线MN交CD于点E，交AB于点F．若AB=6，BC=4，则△ADE的周长为10．

分析 先根据平行四边形的性质得出AB=CD，AD=BC，再由作法可知直线MN是线段AC的垂直平分线，故可得出AE=CE，即AE+DE=CD，据此可得出结论．

解答 解：∵四边形ABCD是平行四边形，
∴AD=BC=4，CD=AB=6，
∵由作法可知，直线MN是线段AC的垂直平分线，
∴AE=CE，
∴AE+DE=CD=6，
∴△ADE的周长=AD+（DE+AE）=4+6=10．
故答案为：10．

点评 本题考查的是作图-基本作图，熟知线段垂直平分线的作法是解答此题的关键．

练习册系列答案
相关题目
7．已知一次函数y=kx+b过（-2，4），且与坐标轴围成的三角形面积为16，求一次函数的解析式．
8．已知关于x的一元二次方程x2-（2k+1）x+k2+2k=0有两个实数根x1，x2，
（1）求实数k的取值范围．
（2）是否存在实数k使得x1x2-x12-x22=-7成立？若存在，请求出k的值；若不存在，请说明理由．
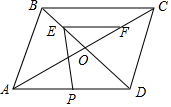5．已知：?ABCD的对角线交于点O，点E，F，P分别是OB，OC，AD的中点，若AC=2AB，求证：EP=EF．
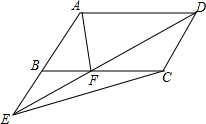12．如图，E是?ABCD中AB延长线上一点，ED交BC于点F，求证：S△ABF=S△CEF．
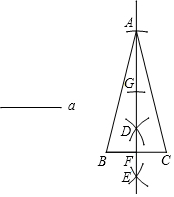2．下面是“已知底边及底边上的高线作等腰三角形”的尺规作图过程．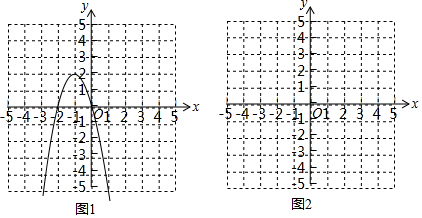
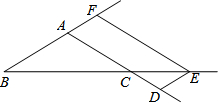已知：线段a．求作：等腰△ABC，使AB=AC，BC=a，BC边上的高为2a．作法：如图，（1）作线段BC=a；（2）作线段BC的垂直平分线DE交BC于点F；（3）在射线FD上顺次截取线段FG=GA=a，连接AB，AC．所以△ABC即为所求作的等腰三角形．
请回答：得到△ABC是等腰三角形的依据是：
①线段垂直平分线上的点到线段两个端点的距离相等：
②有两条边相等的三角形是等腰三角形．
9．根据下列要求，解答相关问题：
（1）请补全以下求不等式-2x2-4x≥0的解集的过程
①构造函数，画出图象：
根据不等式特征构造二次函数y=-2x2-4x；抛物线的对称轴x=-1，开口向下，顶点（-1，2）与x轴的交点是（0，0），（-2，0），用三点法画出二次函数y=-2x2-4x的图象如图1所示；
②数形结合，求得界点：
当y=0时，求得方程-2x2-4x=0的解为x1=0，x2=-2；
③借助图象，写出解集：
由图象可得不等式-2x2-4x≥0的解集为-2≤x≤0．
（2）利用（1）中求不等式解集的方法步骤，求不等式x2-2x+1＜4的解集．
①构造函数，画出图象；
②数形结合，求得界点；
③借助图象，写出解集．
（3）参照以上两个求不等式解集的过程，借助一元二次方程的求根公式，直接写出关于x的不等式ax2+bx+c＞0（a＞0）的解集．
6．在△ABC中，AD=BF，点D，E，F分别是AC，BC，BA延长线上的点，四边形ADEF为平行四边形．
求证：AB=AC．
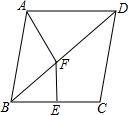7．如图，在菱形ABCD中，∠ABC=40°，BC的垂直平分线EF交对角线BD于点F．连接AF，则∠DAF的度数为120°．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网