题目内容
19．分解因式：（1）（x2+y2）2-4x2y2
（2）25（x-y）2+10（y-x）+1．
分析 （1）先根据平方差公式分解因式，再根据完全平方公式分解因式即可；
（2）根据完全平方公式分解因式即可
解答 解：（1）（x2+y2）2-4x2y2
=（x2+2xy+y2） （x2-2xy+y2）
=（x+y）2（x-y）2；
（2）25（x-y）2+10（y-x）+1
=25（x-y）2-10（x-y）+1
=（5x-5y-1）2．
点评 本题考查了提公因式法与公式法分解因式，要求灵活使用各种方法对多项式进行因式分解，一般来说，如果可以先提取公因式的要先提取公因式，再考虑运用公式法分解．
练习册系列答案
相关题目
1．
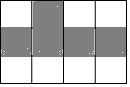如图，共有12个大小相同的小正方形，其中阴影部分的5个小正方形是一个正方体的表面展开图的一部分，现从其余的小正方形中任取一个涂上阴影，能构成这个正方体的表面展开图的概率是（ ）
如图，共有12个大小相同的小正方形，其中阴影部分的5个小正方形是一个正方体的表面展开图的一部分，现从其余的小正方形中任取一个涂上阴影，能构成这个正方体的表面展开图的概率是（ ）| A． | $\frac{4}{7}$ | B． | $\frac{3}{7}$ | C． | $\frac{2}{7}$ | D． | $\frac{1}{7}$ |
2．在平面直角坐标系中，将点A（-1，-2）向右平移3个单位长度得到点B，则点B关于x轴的对称点B′的坐标为（ ）
| A． | （-3，-2） | B． | （2，2） | C． | （-2，2） | D． | （2，-2） |
如图，已知点A是双曲线y=$\frac{{\sqrt{3}}}{x}$在第一象限分支上的一个动点，连结AO并延长交另一分支于点B，以AB为边作等边△ABC，点C在第四象限内，且随着点A的运动，点C的位置也在不断变化，但点C始终在双曲线y=$\frac{k}{x}$上运动，则k的值是-3$\sqrt{3}$．