题目内容
10.解方程组:$\left\{\begin{array}{l}{3u+4v=2,①}\\{2u-v=5,②}\end{array}\right.$.分析 方程组利用加减消元法求出解即可.
解答 解:①+②×4,得11u=22,
解得 u=2,
把u=2代入②解得v=-1,
∴原方程组的解是$\left\{\begin{array}{l}u=2\\ v=-1\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.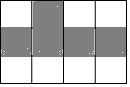 如图,共有12个大小相同的小正方形,其中阴影部分的5个小正方形是一个正方体的表面展开图的一部分,现从其余的小正方形中任取一个涂上阴影,能构成这个正方体的表面展开图的概率是( )
如图,共有12个大小相同的小正方形,其中阴影部分的5个小正方形是一个正方体的表面展开图的一部分,现从其余的小正方形中任取一个涂上阴影,能构成这个正方体的表面展开图的概率是( )
 如图,共有12个大小相同的小正方形,其中阴影部分的5个小正方形是一个正方体的表面展开图的一部分,现从其余的小正方形中任取一个涂上阴影,能构成这个正方体的表面展开图的概率是( )
如图,共有12个大小相同的小正方形,其中阴影部分的5个小正方形是一个正方体的表面展开图的一部分,现从其余的小正方形中任取一个涂上阴影,能构成这个正方体的表面展开图的概率是( )| A. | $\frac{4}{7}$ | B. | $\frac{3}{7}$ | C. | $\frac{2}{7}$ | D. | $\frac{1}{7}$ |
5. 如图,数轴上标有A,B,C,D四个点,其中与表示5-$\sqrt{30}$的点最接近的是( )
如图,数轴上标有A,B,C,D四个点,其中与表示5-$\sqrt{30}$的点最接近的是( )
 如图,数轴上标有A,B,C,D四个点,其中与表示5-$\sqrt{30}$的点最接近的是( )
如图,数轴上标有A,B,C,D四个点,其中与表示5-$\sqrt{30}$的点最接近的是( )| A. | 点A | B. | 点B | C. | 点C | D. | 点D |
15.某机器人公司为扩大经营,决定购进6台机器用于生产某种小机器人.现有甲、乙两种机器供选择,其中每台机器的价格和日生产量如下表所示.经过预算,本次购买机器的费用不能超过34万元.
(1)按要求该公司有几种购买方案?
(2)若该公司购进的6台机器的日生产量不能少于380个,那么为了节约资金,应选择哪种购买方案?
| 甲种机器 | 乙种机器 | |
| 价格/(万元/台) | 5 | 7 |
| 每台机器的日生产量/个 | 60 | 100 |
(2)若该公司购进的6台机器的日生产量不能少于380个,那么为了节约资金,应选择哪种购买方案?
2.在平面直角坐标系中,将点A(-1,-2)向右平移3个单位长度得到点B,则点B关于x轴的对称点B′的坐标为( )
| A. | (-3,-2) | B. | (2,2) | C. | (-2,2) | D. | (2,-2) |
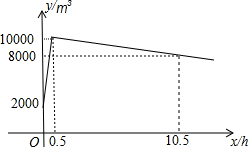 星期天8:00一8:30,燃气公司给平安加气站的储气罐注入天然气.之后,一位工作人员以每车20m3的加气量,依次给在加气站排队等候的若干辆车加气.储气罐中的储气量y(m3)与时间x(h)的函数关系如图所示.
星期天8:00一8:30,燃气公司给平安加气站的储气罐注入天然气.之后,一位工作人员以每车20m3的加气量,依次给在加气站排队等候的若干辆车加气.储气罐中的储气量y(m3)与时间x(h)的函数关系如图所示.