Question

10．如图，某船在A处测得灯塔B在北偏东30°方向，现该船从A处出发以北每小时24海里的速度向正北方向航行15分钟后到达C处，在C处测得灯塔B在北偏东45°的方向，求A到灯塔B的距离．

Answer 1

分析 直接利用锐角三角函数关系得出EB的长，进而得出AB的长．

解答 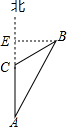解：过点B作BE⊥AC于点E，
∵该船从A处出发以北每小时24海里的速度向正北方向航行15分钟后到达C处，
∴AC=6海里，
∵在C处测得灯塔B在北偏东45°的方向，
∴∠ECB=∠EBC=45°，
∴EC=EB，
∴tan30°=$\frac{EB}{EC+AC}$=$\frac{EB}{EB+6}$=$\frac{\sqrt{3}}{3}$，
解得：EB=3$\sqrt{3}$+3，
则AB=2EB=6$\sqrt{3}$+6，
答：A到灯塔B的距离为（6$\sqrt{3}$+6）海里．

点评 此题主要考查了解直角三角形的应用-方向角，正确得出EB的长是解题关键．