题目内容
9. 如图,已知⊙O的半径为6,M是⊙O外一点,且OM=12,过M的直线与⊙O交于A、B,点A、B关于OM的对称点分别为C、D,AD与BC交于点P,则OP的长为( )
如图,已知⊙O的半径为6,M是⊙O外一点,且OM=12,过M的直线与⊙O交于A、B,点A、B关于OM的对称点分别为C、D,AD与BC交于点P,则OP的长为( )| A. | 4 | B. | 3.5 | C. | 3 | D. | 2.5 |
分析 如图所示,连接AC,MO交于点N,连接OA,OC,根据对称性得到MN⊥AC且AN=CN,根据等腰三角形的性质得到∠APN=∠CPN=∠BPM,根据垂径定理得到∠AON=∠CON=$\frac{1}{2}$∠AOC,由圆周角得到∠AON=∠ABC,推出△AOP∽△MOA,根据相似三角形的性质列方程即可得到结论.
解答  解:如图所示,连接AC,与MO交于点N,连接OA,OC,
解:如图所示,连接AC,与MO交于点N,连接OA,OC,
根据对称性可知:MN⊥AC且AN=CN,
∴点P在MN上;则AP=CP,
∴∠APN=∠CPN,∴∠BPM=∠APO,
根据垂径定理知:∠AON=∠CON=$\frac{1}{2}$∠AOC,
又∠ABC=$\frac{1}{2}$∠AOC(同弧圆周角是圆心角的一半),
∴∠AON=∠ABC,
∵∠AON=180°-(∠OAM+∠AMO),∠ABC=180°-(∠BPM+∠AMO),
∴∠OAM=∠BPM,∴∠OAM=∠APO.又∠AOP=∠MOA,
∵△AOP∽△MOA,
∴$\frac{OP}{OA}$=$\frac{OA}{OM}$;即$\frac{OP}{6}$=$\frac{6}{12}$,
解得:OP=3.
故选C.
点评 本题考查了相似三角形的判定和性质,轴对称的性质,圆周角定理,正确的作出辅助线是解题的关键.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
4. 如图,已知长方体ABCD-EFGH,那么下列直线中与直线BC异面的是( )
如图,已知长方体ABCD-EFGH,那么下列直线中与直线BC异面的是( )
 如图,已知长方体ABCD-EFGH,那么下列直线中与直线BC异面的是( )
如图,已知长方体ABCD-EFGH,那么下列直线中与直线BC异面的是( )| A. | EF | B. | AD | C. | CG | D. | EH |
 如图,某船在A处测得灯塔B在北偏东30°方向,现该船从A处出发以北每小时24海里的速度向正北方向航行15分钟后到达C处,在C处测得灯塔B在北偏东45°的方向,求A到灯塔B的距离.
如图,某船在A处测得灯塔B在北偏东30°方向,现该船从A处出发以北每小时24海里的速度向正北方向航行15分钟后到达C处,在C处测得灯塔B在北偏东45°的方向,求A到灯塔B的距离. 如图,在正方形ABCD中,对角线AC、BD相交于点O,∠BAC的平分线交BD于点G,交BC于点E,过点A作AF⊥AE交CD的延长线于点F,连接EF交BD于点M,若OG+CE=2$\sqrt{7}$,则DM的长为$\frac{2\sqrt{14}}{3}$.
如图,在正方形ABCD中,对角线AC、BD相交于点O,∠BAC的平分线交BD于点G,交BC于点E,过点A作AF⊥AE交CD的延长线于点F,连接EF交BD于点M,若OG+CE=2$\sqrt{7}$,则DM的长为$\frac{2\sqrt{14}}{3}$. 如图,长方形ABCD是由k个相同的长方形组成,上下各有4个水平放置的长方形,中间竖放若干个长方形,并且宽AB是长AD的$\frac{7}{12}$,则k的值为14.
如图,长方形ABCD是由k个相同的长方形组成,上下各有4个水平放置的长方形,中间竖放若干个长方形,并且宽AB是长AD的$\frac{7}{12}$,则k的值为14.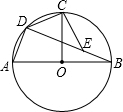 已知AB是⊙O的直径,半径OC⊥AB,D为$\widehat{AC}$上任意一点,E为弦BD上一点,且 BE=AD.
已知AB是⊙O的直径,半径OC⊥AB,D为$\widehat{AC}$上任意一点,E为弦BD上一点,且 BE=AD. 如图,两张48×40的长方形纸片有一个顶点重合,重叠放置的尺寸如图所标示,则图中阴影部分的面积=984.
如图,两张48×40的长方形纸片有一个顶点重合,重叠放置的尺寸如图所标示,则图中阴影部分的面积=984.