题目内容
6.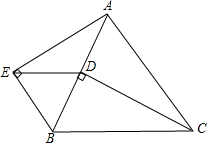 如图,△ABC是等边三角形,CD⊥AB于点D,∠AEB=90°,CD=AE,求证:△EBD是等边三角形.
如图,△ABC是等边三角形,CD⊥AB于点D,∠AEB=90°,CD=AE,求证:△EBD是等边三角形.
分析 首先利用等边三角形的性质证得AB=BC,∠ACD=∠BCD=30°,易得Rt△BCD≌Rt△BAE,由全等三角形的性质可得BD=BE,∠BCD=∠BAE=30°,可得∠ABE=60°,由等边三角形的判定定理易得结论.
解答 证明:∵△ABC是等边三角形,
∴AB=BC,∠ACB=60°,
∵CD⊥AB,
∴∠CDB=90°,∠ACD=∠BCD=30°,
在Rt△BCD和Rt△BAE中,
$\left\{\begin{array}{l}{BC=BA}\\{CD=AE}\end{array}\right.$,
∴Rt△BCD≌Rt△BAE,
∴BD=BE,∠BCD=∠BAE=30°,
∴∠ABE=60°,
∴△EBD为等边三角形.
点评 本题主要考查了等边三角形的判定定理和性质定理,证得Rt△BCD≌Rt△BAE是解答此题的关键.

练习册系列答案
相关题目
14.若点P(a,b)在第二象限,则点P(b,a)在第( )象限.
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
18.如果点M(a+b,ab)在第二象限,那么点N(a,b)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
15.成语所描述的事件为必然事件的是( )
| A. | 水中捞月 | B. | 拔苗助长 | C. | 翁中捉鳖 | D. | 守株待兔 |
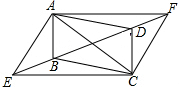 如图,已知四边形AECF是平行四边形,点B,D在对角线EF上,且BE=DF,用向量的加法证明:四边形ABCD是平行四边形.
如图,已知四边形AECF是平行四边形,点B,D在对角线EF上,且BE=DF,用向量的加法证明:四边形ABCD是平行四边形. 在平行四边形ABCD的边AD上任取一点N,过N作平行于对角线AC,BC的直线,分别交边CD,AB于点K、M.证明:△NMB与△NKC等面积.
在平行四边形ABCD的边AD上任取一点N,过N作平行于对角线AC,BC的直线,分别交边CD,AB于点K、M.证明:△NMB与△NKC等面积.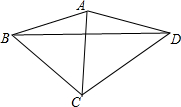 如图,∠ABD=∠ADB=15°,∠CBD=45°,∠CDB=30°.求证:△ABC是等边三角形.
如图,∠ABD=∠ADB=15°,∠CBD=45°,∠CDB=30°.求证:△ABC是等边三角形.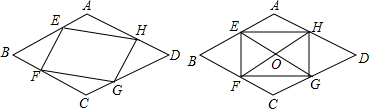
 如图,已知△ACF≌△DBE,且点A,B,C,D在同一条直线上,∠A=50°,∠F=40°.
如图,已知△ACF≌△DBE,且点A,B,C,D在同一条直线上,∠A=50°,∠F=40°.