题目内容
2. 如图,在平行四边形ABCD中,AB⊥AC,点E是AC上一点,且AE=AB,连接BE交BC边上的高AF于点H,延长对角线CA至点G.使AG=CE,连接GH.求证:∠CAD=∠G.
如图,在平行四边形ABCD中,AB⊥AC,点E是AC上一点,且AE=AB,连接BE交BC边上的高AF于点H,延长对角线CA至点G.使AG=CE,连接GH.求证:∠CAD=∠G.
分析 过点A作AK⊥BE交BC于K点,连接AK,EK,HK,根据全等三角形的判定和性质证明即可.
解答 证明:过点A作AK⊥BE交BC于K点,连接AK,EK,HK,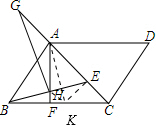
∵AB⊥AC,AE=AB,
∴△ABE是等腰直角三角形,
即∠ABE=∠AEB=45°,
∴∠KAB=∠KAE=∠ABE=∠AEB=45°,
在△KAB与△KAE中$\left\{\begin{array}{l}{AB=AE}\\{∠BAK=∠EAK}\\{AK=AK}\end{array}\right.$,
∴△KAB≌△KAE(SAS),
∴∠KEB=∠KBE,
∵AF⊥BC,
∴∠FAC=∠FBA,
∵∠KBE=∠FBA-∠ABE=∠FAC-∠KAE,
∴∠KBE=∠KAH,
∴∠KEH=∠KBE=∠KAH,
∴∠HAE=∠KEA,
∴∠HAG=∠KEC,
∵∠KEH=∠KAH,
∴点A,E,K,H四点共圆,
即∠EHK=∠KAE=45°,
∴∠EHK=HEA=45°,
∴HK∥CG,
在△KHE与△HKA中$\left\{\begin{array}{l}{∠HAK=∠HEK}\\{∠AKH=∠EHK}\\{HK=KH}\end{array}\right.$,
∴△KHE≌△HKA(AAS),
∴HA=KE,
在△AHG与△EKC中$\left\{\begin{array}{l}{AG=EC}\\{∠GAH=∠CEK}\\{AH=EK}\end{array}\right.$,
∴△AHG≌△EKC(SAS),
∴∠ACB=∠G,
∵四边形ABCD是平行四边形,
∴∠CAD=∠ACB,
∴∠CAD=∠G.
点评 此题主要考查平行四边形的性质和判定以及全等三角形的证明,使学生能够灵活运用平行四边形知识解决有关问题.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
14.若点P(a,b)在第二象限,则点P(b,a)在第( )象限.
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
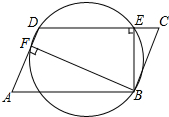 如图,在?ABCD中,BE⊥CD,BF⊥AD,垂足分别是点E,F.求证:B,E,D,F四点都在同一个圆上.
如图,在?ABCD中,BE⊥CD,BF⊥AD,垂足分别是点E,F.求证:B,E,D,F四点都在同一个圆上. 在平行四边形ABCD的边AD上任取一点N,过N作平行于对角线AC,BC的直线,分别交边CD,AB于点K、M.证明:△NMB与△NKC等面积.
在平行四边形ABCD的边AD上任取一点N,过N作平行于对角线AC,BC的直线,分别交边CD,AB于点K、M.证明:△NMB与△NKC等面积.