题目内容
1.两个相似三角形的面积比为1:4,则它们的相似比为( )| A. | 1:4 | B. | 1:2 | C. | 1:16 | D. | 无法确定 |
分析 根据相似三角形面积的比等于相似比的平方解答即可.
解答 解:∵两个相似三角形的面积比为1:4,
∴它们的相似比为1:2,
故选:B.
点评 本题考查的是相似三角形的性质,相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
9.下列几种说法:
①两点之间线段最短;
②任何数的平方都是正数;
③几个角的和等于180°,我们就说这几个角互补;
④34x3是7次单项式;
⑤同旁内角的角平分线相互垂直.
其中正确的语句有( )句.
①两点之间线段最短;
②任何数的平方都是正数;
③几个角的和等于180°,我们就说这几个角互补;
④34x3是7次单项式;
⑤同旁内角的角平分线相互垂直.
其中正确的语句有( )句.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
10.一元二次方程x(2x+3)=5的常数项是( )
| A. | -5 | B. | 2 | C. | 3 | D. | 5 |
11.用10m长的绳子围成长方形,试改变长方形的长度,观察长方形的面积怎样变化,记录不用的矩形的长度值,计算相应的矩形面积的值,探索它们的变化规律,设矩形的长为x m,面积为S m2.
(1)请同学们根据题意填写下表.
(2)在以上这个过程中,变量是x,S,常量是10;
(3)试用含x的式子表示S,S=-x2+10x,x的取值范围是0<x<10;
(4)这个问题反映了矩形的面积随长的变化过程.
(1)请同学们根据题意填写下表.
| 长x(m) | 4 | 3 | 2.5 | 2 | x |
| 另一边长(m) | |||||
| 面积S(m2) |
(3)试用含x的式子表示S,S=-x2+10x,x的取值范围是0<x<10;
(4)这个问题反映了矩形的面积随长的变化过程.
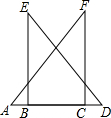 如图,已知△ACF≌△DBE,且点A,B,C,D在同一条直线上,∠A=50°,∠F=40°.
如图,已知△ACF≌△DBE,且点A,B,C,D在同一条直线上,∠A=50°,∠F=40°.