题目内容
6.解下列方程:(1)x(x+1)-5x=0;
(2)$\sqrt{2}$y2=3y;
(3)2(x+1)2=3(x+1);
(4)(x-5)2=(2x+3)2;
(5)(3x-1)2=4(2x+3)2;
(6)(y+3)2-6(y+3)+9=0.
分析 (1)方程利用因式分解法求出解即可;
(2)方程移项后,利用因式分解法求出解即可;
(3)方程移项后,利用因式分解法求出解即可;
(4)方程利用两数的平方相等,两数相等或互为相反数求出解即可;
(5)方程利用两数的平方相等,两数相等或互为相反数求出解即可;
(6)方程利用因式分解法求出解即可.
解答 解:(1)分解因式得:x(x+1-5)=0,
解得:x1=0,x2=4;
(2)方程整理得:$\sqrt{2}$y2-3y=0,即y($\sqrt{2}$y-3)=0,
解得:y1=0,y2=$\frac{3\sqrt{2}}{2}$;
(3)方程整理得:2(x+1)2-3(x+1)=0,
分解因式得:(x+1)(2x+2-3)=0,
解得:x1=-1,x2=$\frac{1}{2}$;
(4)开方得:x-5=2x+3或x-5=-2x-3,
解得:x1=-8,x2=$\frac{2}{3}$;
(5)开方得:3x-1=2(2x+3)或3x-1=-2(2x+3),
解得:x1=-7,x2=-$\frac{5}{7}$;
(6)分解因式得:(y+3-3)2=0,
开方得:y1=y2=0.
点评 此题考查了解一元二次方程-因式分解法,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 如图,在?ABCD中,AB=4cm,AD=6cm,∠BAD的平分线交BC于点E,交DC延长线于点F,则BE:CE=2:1.
如图,在?ABCD中,AB=4cm,AD=6cm,∠BAD的平分线交BC于点E,交DC延长线于点F,则BE:CE=2:1.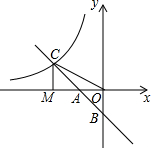 如图,在直角坐标系中,直线y1=-x-l与坐标轴交于A,B两点,与双曲线y2=$\frac{k}{x}$交于点C,连结OC,过点C作CM⊥x轴,垂足为点M,且OA=AM.则下列结论正确的个数是( )
如图,在直角坐标系中,直线y1=-x-l与坐标轴交于A,B两点,与双曲线y2=$\frac{k}{x}$交于点C,连结OC,过点C作CM⊥x轴,垂足为点M,且OA=AM.则下列结论正确的个数是( )