题目内容
11. 如图,在?ABCD中,AB=4cm,AD=6cm,∠BAD的平分线交BC于点E,交DC延长线于点F,则BE:CE=2:1.
如图,在?ABCD中,AB=4cm,AD=6cm,∠BAD的平分线交BC于点E,交DC延长线于点F,则BE:CE=2:1.
分析 先用平行四边形的性质得出∠BAF=∠F,再用角平分线的定义得出∠BAF=∠DAF,进而得出∠DAF=∠F,求出CF=2,最后用平行线得出比例式$\frac{BE}{CE}=\frac{AB}{CF}$=$\frac{4}{2}$=$\frac{1}{2}$.
解答 解:在平行四边形ABCD中,CD=AB=4,BC=AD=6,AB∥CD,
∴∠BAF=∠F,
∵∠BAD的平分线交BC于点E,
∴∠BAF=∠DAF,
∴∠DAF=∠F,
∴DF=AD=6,
∴CF=DF-CD=6-4=2,
∵AB∥CD,
∴$\frac{BE}{CE}=\frac{AB}{CF}$=$\frac{4}{2}$=$\frac{1}{2}$,
故答案为:2:1.
点评 此题是相似三角形的判定和性质,主要考查了角平分线的定义,平行线分线段成比例定理,等腰三角形的判定和性质,解本题的关键是判断出DF=AD.

练习册系列答案
相关题目
1.在⊙O上有顺次三点A,B,C,且$\widehat{AB}$=$\widehat{BC}$=$\widehat{CA}$,则△ABC的形状是( )
| A. | 等腰三角形 | B. | 直角三角形 | C. | 等边三角形 | D. | 等腰直角三角形 |
3.某批乒乓球的质量检验结果如表:
从这批乒乓球中,任意抽取一只乒乓球是优等品的概率的估计值是0.95.(精确到0.01)
| 抽取的乒乓球数n | 50 | 100 | 200 | 500 | 1000 | 1500 | 2000 |
| 优等品的频数m | 48 | 95 | 188 | 471 | 946 | 1426 | 1898 |
| 优等品的频率$\frac{m}{n}$ | 0.960 | 0.950 | 0.940 | 0.942 | 0.946 | 0.951 | 0.949 |
 如图,四边形ABCD中,AB≠CD,E、F、G、H分别是AB、BD、CD、AC的中点.
如图,四边形ABCD中,AB≠CD,E、F、G、H分别是AB、BD、CD、AC的中点. 如图,在直角△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边,若a、b满足方程组$\left\{\begin{array}{l}{b-6=0}\\{2a-b=10}\end{array}\right.$,且c是不等式2x+2>3(x-3)的最大整数解.
如图,在直角△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边,若a、b满足方程组$\left\{\begin{array}{l}{b-6=0}\\{2a-b=10}\end{array}\right.$,且c是不等式2x+2>3(x-3)的最大整数解.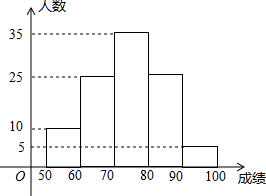 某校八年级同学进行物理知识竞赛,从中随机抽取100人的成绩进行整理,每个小组的分组标准是:50≤x<60,60≤x<70…,画出频数分布直方图如下:
某校八年级同学进行物理知识竞赛,从中随机抽取100人的成绩进行整理,每个小组的分组标准是:50≤x<60,60≤x<70…,画出频数分布直方图如下: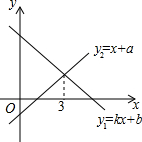 一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①当x<3时,y1>0;②当x<3时,y2>0;③当x>3时,y1<y2中,正确的个数是( )
一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①当x<3时,y1>0;②当x<3时,y2>0;③当x>3时,y1<y2中,正确的个数是( )