��Ŀ����
1����֪������y=ax2+��b+1��x+b-1��a��0����ֱ��y=-x+$\frac{a}{5{a}^{2}-4a+1}$�����壺������ijһ��x0��ʹ�õ㣨x0��x0����������y=ax2+��b+1��x+b-1��a��0���ϣ����x0�������ߵ�һ�������㣮
��1����a=1��b=-2ʱ���������ߵIJ����㣻
��2�����������bֵ�������ߺ������������㣬��a��ȡֵ��Χ��
��3���ڣ�2���������£���A��B����ĺ������������ߵIJ����㣬��AB���е�C��ֱ���ϣ���ֱ��д��b����Сֵ��
���� ��1������������߽���ʽ����ȷ���������ߵIJ����㣻
��2������һԪ���η��̸����б�ʽȷ����a�ķ�Χ��
��3�������е�����ȷ����a��b�ĺ�����ϵʽ���Ӷ����b����Сֵ��
��� �⣺��1����a=1��b=-2ʱ��������y=x2-x-3��
��x2-x-3=x����x2-2x-3=0�����x1=-1��x2=3��
���Դ�ʱ�����ߵIJ�����Ϊ-1��3��
��2�����������bֵ�������ߺ������������㣬
����ax2+��b+1��x+b-1=x
��ax2+bx+b-1=0������������ʵ���⣬
�����=b2-4a��b-1����0�������bֵ�������
��b2-4ab+4a��0�������bֵ�������
���'=��4a��2-4•4a��0
��a2-a��0���0��a��1��
��3����A��x1��x1����B��x2��x2����x1��x2��
��AB���е�C��ֱ���ϣ�
��$\frac{{x}_{1}+{x}_{2}}{2}=-\frac{{x}_{1}+{x}_{2}}{2}+\frac{a}{5{a}^{2}-4a+1}$
��x1+x2=$\frac{a}{5{a}^{2}-4a+1}$
��x1��x2�Ƿ���ax2+bx+b-1=0������
��x1+x2=-$\frac{b}{a}$��
��-$\frac{b}{a}=\frac{a}{5{a}^{2}-4a+1}$
��b=-$\frac{1}{��\frac{1}{a}-2��^{2}+1}$
�൱a=$\frac{1}{2}$ʱ��b����Сֵ��-1��
���� �����Ƕ��κ����ۺ��⣬��Ҫ�������¶��壬һԪ���η��̸����б�ʽ���е����꣬�����¶����ǽⱾ��Ĺؼ���

 ��У����ϵ�д�
��У����ϵ�д�| A�� | ��������� | B�� | ������� | C�� | ֻ�и����� | D�� | ��ͷ��� |
 ��ͼ����?ABCD�У���C=120�㣬CD=4�������²�����ͼ��
��ͼ����?ABCD�У���C=120�㣬CD=4�������²�����ͼ��
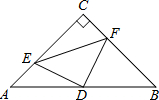 ��ͼ����ABC�ǵ��������Σ���C=90�㣬D��AB���е㣬��E��F�ֱ���AC��BC�����˶�����E�����A��C�غϣ����ұ���AE=CF������DE��DF��EF���ڴ��˶��仯�����У������н��ۣ�
��ͼ����ABC�ǵ��������Σ���C=90�㣬D��AB���е㣬��E��F�ֱ���AC��BC�����˶�����E�����A��C�غϣ����ұ���AE=CF������DE��DF��EF���ڴ��˶��仯�����У������н��ۣ� ��ͼ������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O��DE��AC��CE��BD����֤���ı���OCED�����Σ�
��ͼ������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O��DE��AC��CE��BD����֤���ı���OCED�����Σ�