题目内容
7. 如图,线段AB的长为$30\sqrt{2}$,点D在AB上,△ACD是边长为15的等边三角形,过点D作与CD垂直的射线DP,过DP上一动点G(不与D重合)作矩形CDGH,记矩形CDGH的对角线交点为O,连接OB,则线段BO的最小值为( )
如图,线段AB的长为$30\sqrt{2}$,点D在AB上,△ACD是边长为15的等边三角形,过点D作与CD垂直的射线DP,过DP上一动点G(不与D重合)作矩形CDGH,记矩形CDGH的对角线交点为O,连接OB,则线段BO的最小值为( )| A. | $15\sqrt{2}$ | B. | 15 | C. | $30\sqrt{2}$ | D. | 30 |
分析 根据题意可以知道当BO与DP垂直时,BO取得最小值,此时BO的长度等于BD•sin∠PDB与CD的一半的和,本题得以解决.
解答 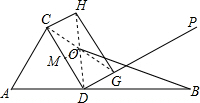 解:如果,作射线MO⊥CD,则点M为CD的中点,
解:如果,作射线MO⊥CD,则点M为CD的中点,
由题意可得,点O为矩形CDGH的中点,所以无论G在射线DP上如何变化,O点的运动轨迹在CD的中垂线上,即O点在射线MO上.
∵DP⊥CD,
∴MO∥DP
线段BO的最小值为B到射线MO的最小距离,所以当BO⊥DP时,BO取得最小值,
∵△ACD是边长为15的等边三角形,四边形CDGH是矩形,
∴∠PDB=180°-60°-90°=30°,线段AB的长为$30\sqrt{2}$,
∴BD=AB-AD=30$\sqrt{2}-15$,
∴BO的最小值是:BD•sin30°+$\frac{15}{2}$=(30$\sqrt{2}$-15)×$\frac{1}{2}$+$\frac{15}{2}$=15$\sqrt{2}$,
故选A.
点评 本题考查矩形的性质、线段的垂直平分线的性质和含30°角的直角三角形,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
19. 如图,一次函数y=-kx+n(k≠0)与x轴、y轴分别交于A、B两点,与反比例函数y=$\frac{k}{x}$(k≠0)交于C、D两点,且C、D两点分别是线段AB的三等分点,若S△AOB=$\frac{9}{4}$,则n=( )
如图,一次函数y=-kx+n(k≠0)与x轴、y轴分别交于A、B两点,与反比例函数y=$\frac{k}{x}$(k≠0)交于C、D两点,且C、D两点分别是线段AB的三等分点,若S△AOB=$\frac{9}{4}$,则n=( )
 如图,一次函数y=-kx+n(k≠0)与x轴、y轴分别交于A、B两点,与反比例函数y=$\frac{k}{x}$(k≠0)交于C、D两点,且C、D两点分别是线段AB的三等分点,若S△AOB=$\frac{9}{4}$,则n=( )
如图,一次函数y=-kx+n(k≠0)与x轴、y轴分别交于A、B两点,与反比例函数y=$\frac{k}{x}$(k≠0)交于C、D两点,且C、D两点分别是线段AB的三等分点,若S△AOB=$\frac{9}{4}$,则n=( )| A. | -$\sqrt{2}$ | B. | -$\frac{3}{2}\sqrt{2}$ | C. | -2$\sqrt{2}$ | D. | -$\frac{5}{2}\sqrt{2}$ |
 已知:线段a和∠α(如图),求作:等腰三角形ABC,使AB=AC,∠B=∠α,高AD=α.
已知:线段a和∠α(如图),求作:等腰三角形ABC,使AB=AC,∠B=∠α,高AD=α. 如图,矩形ABCD的对角线AC、BD相交于点0,过点O作OE⊥AC交AB于E.若BC=8,△AOE的面积为20,则sin∠BOE的值为$\frac{3}{5}$.
如图,矩形ABCD的对角线AC、BD相交于点0,过点O作OE⊥AC交AB于E.若BC=8,△AOE的面积为20,则sin∠BOE的值为$\frac{3}{5}$.
 如图所示,有以下三个条件:①AC=AB,②AB∥CD,③∠1=∠2,从这三个条件中任选两个作为假设,另一个作为结论,则组成真命题的个数为( )
如图所示,有以下三个条件:①AC=AB,②AB∥CD,③∠1=∠2,从这三个条件中任选两个作为假设,另一个作为结论,则组成真命题的个数为( )