题目内容
18.已知x,y满足x2+y2+$\frac{5}{4}$=2x+y,求代数式xy的值.分析 首先移项,分组利用配方法化为完全平方式,利用非负数的性质求得x、y,进一步代入求得数值即可.
解答 解:∵x2+y2+$\frac{5}{4}$=2x+y,
∴x2-2x+1+y2-y+$\frac{1}{4}$=0,
∴(x-1)2+(y-$\frac{1}{2}$)2=0,
∴x-1=0,y-$\frac{1}{2}$=0,
∴x=1,y=$\frac{1}{2}$,
则xy=$\frac{1}{2}$.
点评 此题考查配方法的运用,非负数的性质,掌握完全平方公式是解决问题的关键.

练习册系列答案
相关题目
9. 如图,⊙O是Rt△ABC的外接圆,E是AC的中点,过E作EF⊥AB于D,交⊙O于F,交AC于M,则下列结论:①AM=ME;②DE=$\frac{1}{2}$AC;③DM=$\frac{1}{2}$EM;④OD=$\frac{1}{2}$BC,其中正确结论的序号是( )
如图,⊙O是Rt△ABC的外接圆,E是AC的中点,过E作EF⊥AB于D,交⊙O于F,交AC于M,则下列结论:①AM=ME;②DE=$\frac{1}{2}$AC;③DM=$\frac{1}{2}$EM;④OD=$\frac{1}{2}$BC,其中正确结论的序号是( )
 如图,⊙O是Rt△ABC的外接圆,E是AC的中点,过E作EF⊥AB于D,交⊙O于F,交AC于M,则下列结论:①AM=ME;②DE=$\frac{1}{2}$AC;③DM=$\frac{1}{2}$EM;④OD=$\frac{1}{2}$BC,其中正确结论的序号是( )
如图,⊙O是Rt△ABC的外接圆,E是AC的中点,过E作EF⊥AB于D,交⊙O于F,交AC于M,则下列结论:①AM=ME;②DE=$\frac{1}{2}$AC;③DM=$\frac{1}{2}$EM;④OD=$\frac{1}{2}$BC,其中正确结论的序号是( )| A. | ①②③ | B. | ②③④ | C. | ①③④ | D. | ①②④ |
13.下列计算正确的是( )
| A. | (-p2q)3=-p5q3 | B. | 3m2÷(3m-1)=m-3m2 | ||
| C. | 15a2b3c÷($\frac{15}{2}$ab2)=2ab | D. | (x2-4x)x-1=x-4 |
7. 如图,线段AB的长为$30\sqrt{2}$,点D在AB上,△ACD是边长为15的等边三角形,过点D作与CD垂直的射线DP,过DP上一动点G(不与D重合)作矩形CDGH,记矩形CDGH的对角线交点为O,连接OB,则线段BO的最小值为( )
如图,线段AB的长为$30\sqrt{2}$,点D在AB上,△ACD是边长为15的等边三角形,过点D作与CD垂直的射线DP,过DP上一动点G(不与D重合)作矩形CDGH,记矩形CDGH的对角线交点为O,连接OB,则线段BO的最小值为( )
 如图,线段AB的长为$30\sqrt{2}$,点D在AB上,△ACD是边长为15的等边三角形,过点D作与CD垂直的射线DP,过DP上一动点G(不与D重合)作矩形CDGH,记矩形CDGH的对角线交点为O,连接OB,则线段BO的最小值为( )
如图,线段AB的长为$30\sqrt{2}$,点D在AB上,△ACD是边长为15的等边三角形,过点D作与CD垂直的射线DP,过DP上一动点G(不与D重合)作矩形CDGH,记矩形CDGH的对角线交点为O,连接OB,则线段BO的最小值为( )| A. | $15\sqrt{2}$ | B. | 15 | C. | $30\sqrt{2}$ | D. | 30 |
8.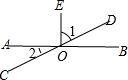 如图,直线AB和CD相交于O点,∠EOB=90°,则图中∠1与∠2的关系是( )
如图,直线AB和CD相交于O点,∠EOB=90°,则图中∠1与∠2的关系是( )
 如图,直线AB和CD相交于O点,∠EOB=90°,则图中∠1与∠2的关系是( )
如图,直线AB和CD相交于O点,∠EOB=90°,则图中∠1与∠2的关系是( )| A. | ∠1与∠2互补 | B. | ∠1与∠2互余 | C. | ∠1与∠2相等 | D. | ∠1=2∠2 |
 如图,在7×7网格中,每个小正方形的边长都为1.
如图,在7×7网格中,每个小正方形的边长都为1.