Question

2．如图，矩形ABCD的对角线AC、BD相交于点0，过点O作OE⊥AC交AB于E．若BC=8，△AOE的面积为20，则sin∠BOE的值为$\frac{3}{5}$．

Answer 1

分析 由题意可知，OE为对角线AC的中垂线，则CE=AE，S_△AEC=2S_△AOE=40，由S_△AEC求出线段AE的长度，进而在Rt△BCE中，由勾股定理求出线段BE的长度；然后证明∠BOE=∠BCE，从而可求得结果．

解答 解：如图，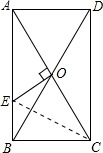

连接EC．
由题意可得，OE为对角线AC的垂直平分线，
∴CE=AE，S_△AOE=S_△COE=5，
∴S_△AEC=2S_△AOE=20．
∴$\frac{1}{2}$AE•BC=20，又BC=8，
∴AE=5，
∴EC=5．
在Rt△BCE中，由勾股定理得：BE=$\sqrt{C{E}^{2}-B{C}^{2}}$=3．
∵∠AEO+∠EAO=90°，∠AEO=∠BOE+∠ABO，
∴∠BOE+∠ABO+∠EAO=90°，又∠ABO=90°-∠OBC=90°-（∠BCE+∠ECO）
∴∠BOE+[90°-（∠BCE+∠ECO）]+∠EAO=90°，
化简得：∠BOE-∠BCE-∠ECO+∠EAO=0，
∵OE为AC中垂线，
∴∠EAO=∠ECO．
代入上式得：∠BOE=∠BCE．
∴sin∠BOE=sin∠BCE=$\frac{BE}{BC}$=$\frac{3}{5}$．
故答案为：$\frac{3}{5}$．

点评 此题考查矩形性质、线段垂直平分线的性质、勾股定理、三角函数的定义等知识点；解题要抓住两个关键：（1）求出线段AE的长度；（2）证明∠BOE=∠BCE．