题目内容
18．（1）抛物线C1：y=（x+1）2-2绕坐标原点O旋转180°得抛物线C2，即：C1，C2关于坐标原点中心对称，则C2的解析式是：y=-（x-1）2+2；（2）若两抛物线关于坐标原点中心对称，且一条抛物线的顶点在另一条抛物线上，我们称这两条抛物线为“共轭抛物线”
①（1）中的C1，C2是否为“共轭抛物线”？
②抛物线M：y=x2+bx+c的顶点坐标是（m，n），若抛物线M与它关于原点中心对称的图形是“共轭抛物线”，求n与m的函数关系式．
分析 （1）根据原抛物线的顶点坐标求出旋转后的抛物线的顶点坐标，然后根据顶点式解析式形式写出即可．
（2）①把抛物线C2的顶点坐标代入抛物线C1的解析式进行验证；
②把抛物线M的共轭抛物线的顶点坐标代入y=x2+bx+c，通过整理可以得到m与n的函数关系式．
解答 解：（1）∵二次函数y=（x+1）2-2的顶点坐标为（-1，-2），
∴绕坐标原点O旋转180°后的抛物线C2的顶点坐标为（1，2），
又∵旋转后抛物线的开口方向上，
∴旋转后的抛物线的解析式为y=-（x-1）2+2．
故答案是：y=-（x-1）2+2．
（2）①由（1）知，抛物线C2的顶点坐标为（1，2）．
把x=1代入抛物线C1：y=（x+1）2-2，得
y=（1+1）2-2=2，即抛物线的顶点C2在抛物线上C1，则两条抛物线为“共轭抛物线”；
②（m，n）关于原点对称的坐标为（-m，-n），共轭抛物线：y=-（x+m）2-n，把（m，n）代入得n=-（2m）2-n，
整理得：n=-2m2．
点评 本题考查了二次函数图象与几何变换，此类题目，利用顶点的变化确定抛物线解析式更简便．
练习册系列答案
相关题目
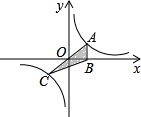如图．正比例函数y=kx与反比例函数y=$\frac{m}{x}$的图象相交于A（1，a）、C（b，-1）两点，过A作x轴的垂线交x轴于B，连BC．