题目内容
19．
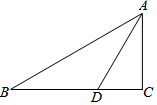如图，△ABC中，∠C=90?，AD平分∠BAC，∠ADB=120°，AD=$2\sqrt{3}$．求AB的长．
分析 由AD平分∠BAC、∠ADB=120°知∠DAC=∠BAD=30°、CD=$\frac{1}{2}AD$=$\sqrt{3}$，由∠DBA=∠DAB=30°知BD=AD=$2\sqrt{3}$，根据sin60°=$\frac{AC}{AD}$得AC的长，从而可得AB=2AC=6．
解答 解：∵∠ADB=120°，
∴∠ADC=60°，∠DAC=30°，
∵AD平分∠BAC，
∴∠DAC=∠BAD=30°，
∴CD=$\frac{1}{2}AD$=$\sqrt{3}$，
∴∠DBA=∠DAB=30°，
∴BD=AD=$2\sqrt{3}$，
∵sin60°=$\frac{AC}{AD}$，
∴$\frac{AC}{{2\sqrt{3}}}=\frac{{\sqrt{3}}}{2}$，
∴AC=3，
∵∠DBA=30°，
∴AB=2AC=6．
点评 本题主要考查角平分线的性质、解直角三角形的应用，熟练掌握三角函数的定义及角平分线的性质得出角的度数是解题的关键．
练习册系列答案
相关题目
1．某商场购进一批服装，每件进价为1000元，由于换季滞销，商场决定将这种服装重新标价后按标价的7折销售．若想打折后每件服装仍能获利5%，该服装的标价应是（ ）
| A． | 1500元 | B． | 1400元 | C． | 1300元 | D． | 1200元 |
如图所示，⊙O的直径AB和弦CD交于E，已知AE=8，EB=2，∠CEA=30°，求CD的长．
如图，在Rt△ABC中，∠BAC=90°，AG⊥BC于G，BD平分∠ABC，AE⊥BD于H，交BC于E，AG交BD于F，连接EF．求证：
如图，⊙C过原点，与x轴、y轴分别交于A、D两点，已知cos∠ABO=$\frac{\sqrt{3}}{2}$，⊙C半径是2，则OD的长为2$\sqrt{3}$．
已知半径为5的⊙O1过点O（0，0），A（8，0），与y轴的正半轴交于点B，OE为直径，点M为弧OBE上一动点（不与点O、E重合），连结MA，作NA⊥MA于点A交ME的延长线于点N，则线段AN最长为$\frac{15}{2}$．
Rt△ABC中∠C=90°，AC=4，cosB=$\frac{3}{5}$，半径为r的⊙C与△ABC的边有两个交点，则r的取值范围是0＜r＜2.4．