题目内容
9. Rt△ABC中∠C=90°,AC=4,cosB=$\frac{3}{5}$,半径为r的⊙C与△ABC的边有两个交点,则r的取值范围是0<r<2.4.
Rt△ABC中∠C=90°,AC=4,cosB=$\frac{3}{5}$,半径为r的⊙C与△ABC的边有两个交点,则r的取值范围是0<r<2.4.
分析 由题意可知:当AB与⊙C相离时⊙C与△ABC的边有两个交点,作CD⊥AB于点D,求得高CD的长,继而求得答案.
解答 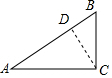 解:由题意可知:当AB与⊙C相离时⊙C与△ABC的边有两个交点,
解:由题意可知:当AB与⊙C相离时⊙C与△ABC的边有两个交点,
∵Rt△ABC中∠C=90°,AC=4,cosB=$\frac{3}{5}$,
∴$\frac{BC}{AB}$=$\frac{3}{5}$,
∴AB=5,BC=3,
作CD⊥AB于点D,
∵$\frac{1}{2}$AB•CD=$\frac{1}{2}$AC•BC
∴CD=$\frac{AC•BC}{AB}$=2.4,
∴半径为r的⊙C与△ABC的边有两个交点,则r的取值范围是:r<2.4.
故答案为:0<r<2.4.
点评 此题考查了直线与圆的位置关系、勾股定理以及直角三角形的性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
17. 如图,直线y=$\frac{4}{3}$x-4与x轴、y轴分别交于A、B两点,把△AOB以x轴为对称轴翻折得到△AOB′,再将△AOB′绕点A顺时针旋转90°,得到△AO′B″,则点B″的坐标是( )
如图,直线y=$\frac{4}{3}$x-4与x轴、y轴分别交于A、B两点,把△AOB以x轴为对称轴翻折得到△AOB′,再将△AOB′绕点A顺时针旋转90°,得到△AO′B″,则点B″的坐标是( )
 如图,直线y=$\frac{4}{3}$x-4与x轴、y轴分别交于A、B两点,把△AOB以x轴为对称轴翻折得到△AOB′,再将△AOB′绕点A顺时针旋转90°,得到△AO′B″,则点B″的坐标是( )
如图,直线y=$\frac{4}{3}$x-4与x轴、y轴分别交于A、B两点,把△AOB以x轴为对称轴翻折得到△AOB′,再将△AOB′绕点A顺时针旋转90°,得到△AO′B″,则点B″的坐标是( )| A. | (3,4) | B. | (4,4) | C. | (7,3) | D. | (7,4) |
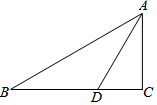 如图,△ABC中,∠C=90?,AD平分∠BAC,∠ADB=120°,AD=$2\sqrt{3}$.求AB的长.
如图,△ABC中,∠C=90?,AD平分∠BAC,∠ADB=120°,AD=$2\sqrt{3}$.求AB的长.
 如图,△ABC为一个直角三角形的空地,∠C为直角,AC边长为3百米,BC边长为4百米,现决定在空地内筑一条笔直的路EF(宽度不计),E为BC的中点,F为三角形ABC边上的一点,且EF将该空地分成一个四边形和一个三角形,若分成的四边形和三角形周长相等,求此时小路EF的长度.
如图,△ABC为一个直角三角形的空地,∠C为直角,AC边长为3百米,BC边长为4百米,现决定在空地内筑一条笔直的路EF(宽度不计),E为BC的中点,F为三角形ABC边上的一点,且EF将该空地分成一个四边形和一个三角形,若分成的四边形和三角形周长相等,求此时小路EF的长度. 如图,正六边形ABCDEF,连结AC,求作点P,Q使它们成为AC的三等分点,下列作法正确的是( )
如图,正六边形ABCDEF,连结AC,求作点P,Q使它们成为AC的三等分点,下列作法正确的是( ) 如图,在△ABC中,∠A:∠ABC:∠ACB=3:5:10,B′为AC延长线上一点,A′是B′B延长线上一点,且△A′B′C≌△ABC,则∠BCA′:∠BCB′=1:4.
如图,在△ABC中,∠A:∠ABC:∠ACB=3:5:10,B′为AC延长线上一点,A′是B′B延长线上一点,且△A′B′C≌△ABC,则∠BCA′:∠BCB′=1:4.