题目内容
7.请你从x2-1,x2+2x+1,x2+x中任意选取两个,将其中一个作为分子,另一个作为分母,组成一个分式,并将这个分式化简,再求当x=2时分式的值.分析 结合题意,先选取两个式子组成分式,然后进行化简并将x=2的值代入求解.
解答 解:选取x2-1为为分子,x2+2x+1为分母,组成分式为:$\frac{{x}^{2}-1}{{x}^{2}+2x+1}$,
将这个分式化简,
原式=$\frac{(x+1)(x-1)}{(x+1)^{2}}$
=$\frac{x-1}{x+1}$.
当x=2时,
原式=$\frac{2-1}{2+1}$=$\frac{1}{3}$.
点评 本题考查了分式的化简求值,解答本题的关键在于结合题意,先选取两个式子组成分式,然后进行化简并将x=2的值代入求解.

练习册系列答案
相关题目
9.如图所示,图(1)表示 1 张餐桌和 6 张椅子(三角形表示餐桌,每个小圆表示一张椅子),图(2)表示 2 张餐桌和 8 张椅子,图(3)表示 3 张餐桌和 10 张椅子…;若按这种方式摆放 25 张桌子需要的椅子张数是( )
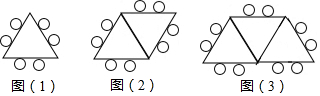

| A. | 25 张 | B. | 50 张 | C. | 54 张 | D. | 150 张 |
17. 如图,直线y=$\frac{4}{3}$x-4与x轴、y轴分别交于A、B两点,把△AOB以x轴为对称轴翻折得到△AOB′,再将△AOB′绕点A顺时针旋转90°,得到△AO′B″,则点B″的坐标是( )
如图,直线y=$\frac{4}{3}$x-4与x轴、y轴分别交于A、B两点,把△AOB以x轴为对称轴翻折得到△AOB′,再将△AOB′绕点A顺时针旋转90°,得到△AO′B″,则点B″的坐标是( )
 如图,直线y=$\frac{4}{3}$x-4与x轴、y轴分别交于A、B两点,把△AOB以x轴为对称轴翻折得到△AOB′,再将△AOB′绕点A顺时针旋转90°,得到△AO′B″,则点B″的坐标是( )
如图,直线y=$\frac{4}{3}$x-4与x轴、y轴分别交于A、B两点,把△AOB以x轴为对称轴翻折得到△AOB′,再将△AOB′绕点A顺时针旋转90°,得到△AO′B″,则点B″的坐标是( )| A. | (3,4) | B. | (4,4) | C. | (7,3) | D. | (7,4) |
 如图,每个小正方形的边长为1,A、B、C为小正方形的顶点,求证:∠ABC=45°.
如图,每个小正方形的边长为1,A、B、C为小正方形的顶点,求证:∠ABC=45°.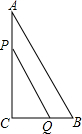 如图,△ABC中,∠C=90°,BC=5厘米,AB=5$\sqrt{5}$厘米,点P从点A出发沿AC边以2厘米/秒的速度向终点C匀速移动,同时,点Q从点C出发沿CB边以1厘米/秒的速度向终点B匀速移动,P、Q两点运动几秒时,P、Q两点间的距离是2$\sqrt{10}$厘米?
如图,△ABC中,∠C=90°,BC=5厘米,AB=5$\sqrt{5}$厘米,点P从点A出发沿AC边以2厘米/秒的速度向终点C匀速移动,同时,点Q从点C出发沿CB边以1厘米/秒的速度向终点B匀速移动,P、Q两点运动几秒时,P、Q两点间的距离是2$\sqrt{10}$厘米?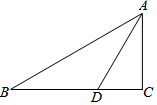 如图,△ABC中,∠C=90?,AD平分∠BAC,∠ADB=120°,AD=$2\sqrt{3}$.求AB的长.
如图,△ABC中,∠C=90?,AD平分∠BAC,∠ADB=120°,AD=$2\sqrt{3}$.求AB的长.