题目内容
10. 如图所示,⊙O的直径AB和弦CD交于E,已知AE=8,EB=2,∠CEA=30°,求CD的长.
如图所示,⊙O的直径AB和弦CD交于E,已知AE=8,EB=2,∠CEA=30°,求CD的长.
分析 根据AE=8cm,EB=2cm,可求出圆的半径=5,从点O向CD作垂线,交点为F则OE=3,再根据勾股定理求CF的长,从而求出CD的长.
解答 解:∵AE=8cm,EB=2cm,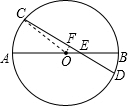
∴OA=(8cm+2cm)÷2=5cm,
∴OE=5cm-2cm=3cm,
过点O作OF⊥CD于F,可得∠OFE=90°,即△OEF为直角三角形,
∵∠CEA=30°,
∴OF=$\frac{1}{2}$OE=$\frac{3}{2}$cm,
连接OC,
在Rt△COF中,CD=2CF=2$\sqrt{O{C}^{2}-O{F}^{2}}$=2$\sqrt{{5}^{2}-(\frac{3}{2})^{2}}$=3$\sqrt{11}$cm.
点评 本题考查了垂径定理,解题关键是作OF⊥CD于F,先求OE,再求OF,最后用勾股定理求CD.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.某学校 2013 年年底调查学生的近视率为15%,经过两年的时间,2015 年年底再次调查该校学生的近视率为 20%,设该校这两年学生人数总数不变,学生近视率年均增长率为 x,则以下所列方程正确的是( )
| A. | (1+x)+15%(1+x)2=20% | B. | 15%(1+x%)2=20% | C. | 15%(1-x)2=20% | D. | 15%(1+x)2=20% |
13.若一个多边形的每一个外角都是45°,则这个多边形是( )
| A. | 六边形 | B. | 七边形 | C. | 八边形 | D. | 九边形 |
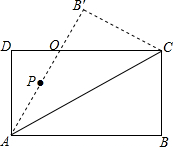 如图,在矩形ABCD中,∠CAB=30°,BC=4$\sqrt{3}$cm,将△ABC沿AC边翻折,使点B到点B′,AB′与DC相交于点O.
如图,在矩形ABCD中,∠CAB=30°,BC=4$\sqrt{3}$cm,将△ABC沿AC边翻折,使点B到点B′,AB′与DC相交于点O. 如图,每个小正方形的边长为1,A、B、C为小正方形的顶点,求证:∠ABC=45°.
如图,每个小正方形的边长为1,A、B、C为小正方形的顶点,求证:∠ABC=45°.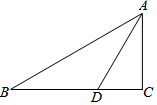 如图,△ABC中,∠C=90?,AD平分∠BAC,∠ADB=120°,AD=$2\sqrt{3}$.求AB的长.
如图,△ABC中,∠C=90?,AD平分∠BAC,∠ADB=120°,AD=$2\sqrt{3}$.求AB的长.