题目内容
8.如图,过正方形ABCD的顶点A作直线l,交边BC于点M,过B、D两点作直线l的垂线,垂足分别为E、F.(1)试求BE、DF、EF之间的数量关系,并说明你的理由.
(2)若以点A为旋转中心旋转直线l,仍过B,D两点作直线l的垂线,则第(1)题中的结论还成立吗?请说明理由.
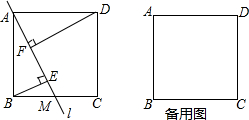
分析 (1)如图1,利用“AAS”证明△ABE≌△ADF,则BE=AF,AE=DF,然后利用EF=AE-AF得到DF-BE=EF;
(2)如图2,证明△ABE≌△ADF得到BE=AF,AE=DF,则利用EF=AF-AE得到BE-DF=EF;如图3,同理可得BE+DF=EF.
解答 解:(1)DF-BE=EF.理由如下:如图1,
∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°,
∵∠BAE+∠DAF=90°,∠BAE+∠ABE=90°,
∴∠ABE=∠DAF,
在△ABE和△ADF中
$\left\{\begin{array}{l}{∠AEB=∠DFA}\\{∠BAE=∠DAF}\\{AB=AD}\end{array}\right.$,
∴△ABE≌△ADF,
∴BE=AF,AE=DF,
∵EF=AE-AF,
∴DF-BE=EF;
(2)第(1)题中的结论不成立.
如图2,同理可证明△ABE≌△ADF,
∴BE=AF,AE=DF,
∵EF=AF-AE,
∴BE-DF=EF;
如图3,同理可证明△ABE≌△ADF,
∴BE=AF,AE=DF,
∵EF=AF+AE,
∴BE+DF=EF.
点评 本题考查了正方形的性质:正方形的四条边都相等,四个角都是直角.解决此题的关键是证明△ABE≌△ADF得到BE=AF,AE=DF,然后利用不同位置得到BE、DF、EF的关系.

练习册系列答案
相关题目
18. 如图,直线AB,CD相交于点O,则∠AOC的度数是( )
如图,直线AB,CD相交于点O,则∠AOC的度数是( )
 如图,直线AB,CD相交于点O,则∠AOC的度数是( )
如图,直线AB,CD相交于点O,则∠AOC的度数是( )| A. | 60° | B. | 40° | C. | 30° | D. | 20° |
 如图,已知AB是⊙O的直径,D是⊙O上一点,弦DE⊥AB于C,弦EF交线段CB于G,求证:BD平分∠FDG.
如图,已知AB是⊙O的直径,D是⊙O上一点,弦DE⊥AB于C,弦EF交线段CB于G,求证:BD平分∠FDG. 如图,甲、乙两船从港口A同时出发,甲船以每小时30海里的速度向北偏东35°方向航行,乙船以每小时40海里的速度向另一方向航行,1小时后,甲船到达C岛,乙船达到B岛,若C、B两岛相距50海里,请你求出乙船的航行方向.
如图,甲、乙两船从港口A同时出发,甲船以每小时30海里的速度向北偏东35°方向航行,乙船以每小时40海里的速度向另一方向航行,1小时后,甲船到达C岛,乙船达到B岛,若C、B两岛相距50海里,请你求出乙船的航行方向. 已知等腰直角△ABC的直角边长与正方形MNPQ的边长均为10cm,CA与MN在同一条直线上,点A从点M开始向右移动,设点A的移动距离为xcm(0≤x≤20),重叠部分的面积为S(cm2).
已知等腰直角△ABC的直角边长与正方形MNPQ的边长均为10cm,CA与MN在同一条直线上,点A从点M开始向右移动,设点A的移动距离为xcm(0≤x≤20),重叠部分的面积为S(cm2).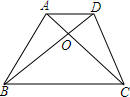 如图,梯形ABCD中,AD∥BC,△AOB的面积是16平方厘米,△AOD的面积是12平方厘米,求:(1)△BOC和△COD面积;(2)$\frac{AO}{AC}$的值.
如图,梯形ABCD中,AD∥BC,△AOB的面积是16平方厘米,△AOD的面积是12平方厘米,求:(1)△BOC和△COD面积;(2)$\frac{AO}{AC}$的值. 如图所示,小明家的观光果园是由两块矩形但重叠了一部分而成的,其重叠部分为正方形,已知果园总面积是116m2,今若将重叠部分改造成休闲区域,求休闲区域的边长.
如图所示,小明家的观光果园是由两块矩形但重叠了一部分而成的,其重叠部分为正方形,已知果园总面积是116m2,今若将重叠部分改造成休闲区域,求休闲区域的边长. 如图,在边长为2的正方形ABCD中,点E是边AD中点,点F在边CD上,且FE⊥BE,设BD与EF交于点G,则△DEG的面积是$\frac{1}{6}$.
如图,在边长为2的正方形ABCD中,点E是边AD中点,点F在边CD上,且FE⊥BE,设BD与EF交于点G,则△DEG的面积是$\frac{1}{6}$.