Question

13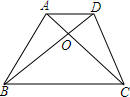．如图，梯形ABCD中，AD∥BC，△AOB的面积是16平方厘米，△AOD的面积是12平方厘米，求：（1）△BOC和△COD面积；（2）$\frac{AO}{AC}$的值．

Answer 1

分析 （1）由梯形ABCD中，AD∥BC，易得S_△ABC=S_△DBC，即可求得△COD面积；又由AD∥BC，可得△AOD∽△COB，然后由相似三角形的面积比等于相似比的平方，求得答案；
（2）由△AOD∽△COB，然后由相似三角形的对应边成比例求得答案．

解答 解：（1）∵梯形ABCD中，AD∥BC，
∴S_△ABC=S_△DBC，
∴S_△COD=S_△AOB=16cm²，
∵△AOB的面积是16平方厘米，△AOD的面积是12平方厘米，
∴OD：OB=S_△AOD：S_△AOB=12：16=3：4，
∵AD∥BC，
∴△AOD∽△COB，
∴S_△AOD：S_△COB=9：16，
∵S_△AOD=12cm²，
∴S_△BOC=$\frac{64}{3}$cm²；

（2）∵△AOD∽△COB，
∴OD：OB=OA：OC，
∴OA：OC=3：4，
∴$\frac{AO}{AC}$=$\frac{3}{7}$．

点评 此题考查了相似三角形的判定与性质．注意相似三角形的面积比等于相似比的平方，等高三角形的面积比等于对应底的比．