题目内容
8.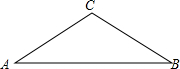 如图,已知在等腰△ABC中,∠A=∠B=30°.
如图,已知在等腰△ABC中,∠A=∠B=30°.(1)尺规作图:过点C作CD⊥AC交AB于点D;过A,D,C三点作⊙O(只要求作出图形,保留痕迹,不要求写作法);
(2)求证:BC2=BD•AB.
分析 (1)利用过直线上一点作直线的垂线确定D点,再作AD的垂直平分线确定AD的中点O,然后以点O为圆心,OA为半径作⊙O即可;
(2)根据圆周角定理,由∠ACD=90°,根据三角形的内角和和等腰三角形的性质得到∠DCB=∠A=30°,推出△CDB∽△ACB,根据相似三角形的性质即可得到结论.
解答 (1)解:如图;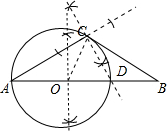
(2)证明:∵CD⊥AC,
∴∠ACD=90°
∵∠A=∠B=30°,
∴∠ACB=120°
∴∠DCB=∠A=30°,
∵∠B=∠B,
∴△CDB∽△ACB,
∴$\frac{BC}{BD}=\frac{AB}{BC}$;
∴BC2=BD•AB.
点评 本题考查了复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了等腰三角形的性质和相似三角形的判定和性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.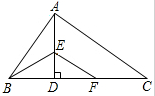 如用,Rt△ABC中,AB⊥AC,AD⊥BC,BE平分∠ABC,交AD于E,EF∥AC,下列结论中:①AB=BF;②AE=ED;③AD=DC;④∠ABE=∠DFE;⑤$\frac{AB}{BD}$=$\frac{CF}{DF}$,正确的是( )
如用,Rt△ABC中,AB⊥AC,AD⊥BC,BE平分∠ABC,交AD于E,EF∥AC,下列结论中:①AB=BF;②AE=ED;③AD=DC;④∠ABE=∠DFE;⑤$\frac{AB}{BD}$=$\frac{CF}{DF}$,正确的是( )
 如用,Rt△ABC中,AB⊥AC,AD⊥BC,BE平分∠ABC,交AD于E,EF∥AC,下列结论中:①AB=BF;②AE=ED;③AD=DC;④∠ABE=∠DFE;⑤$\frac{AB}{BD}$=$\frac{CF}{DF}$,正确的是( )
如用,Rt△ABC中,AB⊥AC,AD⊥BC,BE平分∠ABC,交AD于E,EF∥AC,下列结论中:①AB=BF;②AE=ED;③AD=DC;④∠ABE=∠DFE;⑤$\frac{AB}{BD}$=$\frac{CF}{DF}$,正确的是( )| A. | ①③ | B. | ①⑤ | C. | ③④ | D. | ①②⑤ |
13.某中学八年级同学在综合实践学习课上,做大蒜在相同条件下的发芽实验,结果统计如表,则试验中大蒜发芽的概率估计是0.95(精确到0.01).
| 种子粒数 | 100 | 500 | 1000 | 2000 | 3000 |
| 发芽粒数 | 96 | 470 | 948 | 1912 | 2853 |
| 发芽频率 | 0.96 | 0.94 | 0.948 | 0.956 | 0.951 |
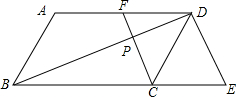 如图,在平行四边形ABCD中,F是AD的中点,延长BC到点E,使CE=$\frac{1}{2}$BC,连结DE、CF,连接BD交CF于点P.
如图,在平行四边形ABCD中,F是AD的中点,延长BC到点E,使CE=$\frac{1}{2}$BC,连结DE、CF,连接BD交CF于点P.