题目内容
4.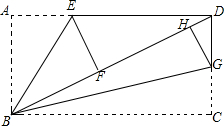 如图,在矩形ABCD中,AB=6,BC=8,E,G分别在AD,CD上,沿BE,BG折叠矩形,点A和点C分别落在BD上的点F,H处.
如图,在矩形ABCD中,AB=6,BC=8,E,G分别在AD,CD上,沿BE,BG折叠矩形,点A和点C分别落在BD上的点F,H处.(1)∠EBG=45度,图中有8对相似三角形;
(2)DE=5,DG=$\frac{10}{3}$;
(3)连结EG,求△BEG的面积.
分析 (1)根据矩形的性质得出∠ABC=90°,AD=BC,AB=CD,根据折叠的性质得出∠ABE=∠DBE,∠CBG=∠DBG,即可求出答案;根据相似三角形的判定得出即可;
(2)根据勾股定理求出BD,证出△EFD∽△BAD,得出$\frac{8-DE}{6}$=$\frac{DE}{10}$,同理$\frac{6-DG}{8}$=$\frac{DG}{10}$,求出即可;
(3)根据图形得出S△BEG=S矩形ABCD-S△ABE-S△BCG-S△CDE,根据面积公式求出即可.
解答 解:(1)∵四边形ABCD是矩形,
∴∠ABC=90°,AD=BC,AB=CD,
根据折叠的性质得出∠ABE=∠DBE,∠CBG=∠DBG,
∴∠EBG=$\frac{1}{2}$∠ABC=45°,
图中的相似三角形有△ABD和△CDB,△EFD和△DAB,△EFD和△DCB,△DHG和△DCB,△DHG和△BAD,△EFD和△DHG,△ABE和△FBE,△GHB和△GCB,共8对,
故答案为:45,8;
(2)∵四边形ABCD是矩形,
∴∠A=90°,AD=BC=8,AB=DC=6,
在Rt△BAD中,由勾股定理得:BD=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵根据折叠得出AE=EF,∠A=∠BFE=90°,
∴∠EFD=∠A=90°,
∵∠EDF=∠BDA,
∴△EFD∽△BAD,
∴$\frac{EF}{AB}$=$\frac{DE}{BD}$,
∴$\frac{8-DE}{6}$=$\frac{DE}{10}$,
解得:DE=5,
同理$\frac{6-DG}{8}$=$\frac{DG}{10}$,
解得:DG=$\frac{10}{3}$,
故答案为:5,$\frac{10}{3}$;
(3)如图,∵AB=DC=6,DG=$\frac{10}{3}$,DE=5,AD=BC=8,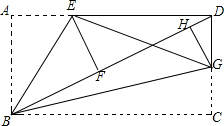
∴AE=8-5=3,CG=6-$\frac{10}{3}$=$\frac{8}{3}$,
∵四边形ABCD是矩形,
∴∠A=∠ABC=∠C=∠ADC=90°,
∴S△BEG=S矩形ABCD-S△ABE-S△BCG-S△CDE
=6×8-$\frac{1}{2}$×6×3-$\frac{1}{2}$×8×$\frac{8}{3}$-$\frac{1}{2}$×5×$\frac{10}{3}$
=18,
即△BEG的面积是18.
点评 本题考查了矩形的性质,相似三角形的性质和判定的应用,能综合运用定理进行推理和计算是解此题的关键.

 名校课堂系列答案
名校课堂系列答案| A. | 2,3,4 | B. | 5,5,10 | C. | 2,2,1 | D. | 1,2,3 |
| 种子粒数 | 100 | 500 | 1000 | 2000 | 3000 |
| 发芽粒数 | 96 | 470 | 948 | 1912 | 2853 |
| 发芽频率 | 0.96 | 0.94 | 0.948 | 0.956 | 0.951 |
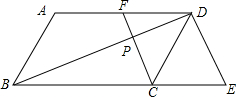 如图,在平行四边形ABCD中,F是AD的中点,延长BC到点E,使CE=$\frac{1}{2}$BC,连结DE、CF,连接BD交CF于点P.
如图,在平行四边形ABCD中,F是AD的中点,延长BC到点E,使CE=$\frac{1}{2}$BC,连结DE、CF,连接BD交CF于点P.