题目内容
13.将x=$\frac{2}{3}$代入反比例函数y=-$\frac{1}{x}$中,所得函数值记为y1,又将x=y1+1代入原反比例函数中,所得函数值记为y2,再将x=y2+1代入原反比例函数中,所得函数值记为y2,…,如此继续下去,则y2013=( )| A. | -$\frac{3}{2}$ | B. | 2 | C. | -$\frac{1}{3}$ | D. | -$\frac{3}{4}$ |
分析 分别计算出y1,y2,y3,y4,可得到每三个一循环,而2013=671,即可得到y2013=y3.
解答 解:将x=$\frac{2}{3}$代入反比例函数y=-$\frac{1}{x}$中,得y1=-$\frac{1}{\frac{2}{3}}$=-$\frac{3}{2}$,
把x=-$\frac{3}{2}$+1=-$\frac{1}{2}$代入反比例函数y=-$\frac{1}{x}$得y2=-$\frac{1}{-\frac{1}{2}}$=2;
把x=2+1=3代入反比例函数y=-$\frac{1}{x}$得y3=-$\frac{1}{3}$;
把x=-$\frac{1}{3}$+1=$\frac{2}{3}$代入反比例函数y=-$\frac{1}{x}$得y4=-$\frac{3}{2}$;…;
如此继续下去每三个一循环,
∵2013÷3=671,
∴y2013=y3=-$\frac{1}{3}$.
故选C.
点评 本题考查了反比例函数的性质:反比例函数y=$\frac{k}{x}$(k≠0)的图象为双曲线,当k>0时,图象发布在第一、三象限,在每一象限,y随x增大而减小;当k<0时,图象发布在第二、四象限,在每一象限,y随x增大而增大;

练习册系列答案
相关题目
3.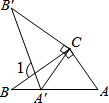 如图,将Rt△ABC以直角顶点C为旋转中心顺时针旋转,使点A刚好落在AB上(即:点A′),若∠A=55°,则图中∠1=( )
如图,将Rt△ABC以直角顶点C为旋转中心顺时针旋转,使点A刚好落在AB上(即:点A′),若∠A=55°,则图中∠1=( )
 如图,将Rt△ABC以直角顶点C为旋转中心顺时针旋转,使点A刚好落在AB上(即:点A′),若∠A=55°,则图中∠1=( )
如图,将Rt△ABC以直角顶点C为旋转中心顺时针旋转,使点A刚好落在AB上(即:点A′),若∠A=55°,则图中∠1=( )| A. | 110° | B. | 102° | C. | 105° | D. | 125° |
5.在一个不透明的口袋中装有颜色分别为红色、白色、绿色的三个小球,这三个小球除颜色外其他都相同,在口袋中一次性随机摸出两个球,下列事件为必然事件的是( )
| A. | 一个红球一个白球 | B. | 两个红球 | ||
| C. | 两个球颜色不相同 | D. | 两个球颜色相同 |
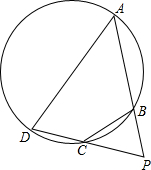 如图,已知ABCD是一个半径为R的圆的内接四边形,AB=12,CD=6,分别延长AB和DC,它们相交于点P,且BP=8,
如图,已知ABCD是一个半径为R的圆的内接四边形,AB=12,CD=6,分别延长AB和DC,它们相交于点P,且BP=8,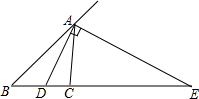 已知:AD、AE分别为△ABC的内、外角平分线,求证:$\frac{1}{BD}$+$\frac{1}{BE}$=$\frac{2}{BC}$.
已知:AD、AE分别为△ABC的内、外角平分线,求证:$\frac{1}{BD}$+$\frac{1}{BE}$=$\frac{2}{BC}$.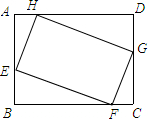 如图,矩形ABCD中,AB=3,BC=4,E、F、G、H分别在四边上,且四边形EFGH为矩形,若EF=2EH,则AE=$\frac{5}{3}$.
如图,矩形ABCD中,AB=3,BC=4,E、F、G、H分别在四边上,且四边形EFGH为矩形,若EF=2EH,则AE=$\frac{5}{3}$.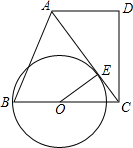 如图,在梯形ABCD中,AD∥BD,DC⊥BC,AB=13,BC=14,AD=9,点O在边BC上,且以O为圆心,OB为半径的⊙O与AC相切于点E
如图,在梯形ABCD中,AD∥BD,DC⊥BC,AB=13,BC=14,AD=9,点O在边BC上,且以O为圆心,OB为半径的⊙O与AC相切于点E