题目内容
3.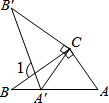 如图,将Rt△ABC以直角顶点C为旋转中心顺时针旋转,使点A刚好落在AB上(即:点A′),若∠A=55°,则图中∠1=( )
如图,将Rt△ABC以直角顶点C为旋转中心顺时针旋转,使点A刚好落在AB上(即:点A′),若∠A=55°,则图中∠1=( )| A. | 110° | B. | 102° | C. | 105° | D. | 125° |
分析 先利用互余计算出∠B=35°,再根据旋转的性质得CA=CA′,∠ACA′=∠BCB′,∠B′=∠B=35°,则利用等腰三角形的性质得∠CA′A=∠CAA′=55°,于是利用三角形内角和可计算出∠ACA′=70°,则∠BCB′=70°,然后根据三角形外角性质计算∠1的度数.
解答 解:在Rt△ABC中,∠B=90°-∠A=35°,
∵Rt△ABC以直角顶点C为旋转中心顺时针旋转,使点A刚好落在AB上(即:点A′),
∴CA=CA′,∠ACA′=∠BCB′,∠B′=∠B=35°,
∴∠CA′A=∠CAA′=55°,
∴∠ACA′=180°-2×55°=70°,
∴∠BCB′=70°,
∴∠1=∠BCB′+∠B′=70°+35°=105°.
故选C.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.

练习册系列答案
相关题目
18.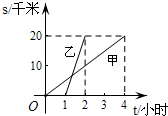 甲、乙两人沿相同的路线由A地到B地匀速前进,A,B两地间的路程为20千米,他们前进的路程为s(单位:千米),甲出发后的时间为t(单位:小时),甲、乙前进的路程与时间的函数图象如图所示.根据图象信息下列说法正确的是( )
甲、乙两人沿相同的路线由A地到B地匀速前进,A,B两地间的路程为20千米,他们前进的路程为s(单位:千米),甲出发后的时间为t(单位:小时),甲、乙前进的路程与时间的函数图象如图所示.根据图象信息下列说法正确的是( )
 甲、乙两人沿相同的路线由A地到B地匀速前进,A,B两地间的路程为20千米,他们前进的路程为s(单位:千米),甲出发后的时间为t(单位:小时),甲、乙前进的路程与时间的函数图象如图所示.根据图象信息下列说法正确的是( )
甲、乙两人沿相同的路线由A地到B地匀速前进,A,B两地间的路程为20千米,他们前进的路程为s(单位:千米),甲出发后的时间为t(单位:小时),甲、乙前进的路程与时间的函数图象如图所示.根据图象信息下列说法正确的是( )| A. | 甲的速度是4千米/小时 | B. | 乙的速度是10千米/小时 | ||
| C. | 乙比甲晚出发1小时 | D. | 甲比乙晚到B地3小时 |
15.下列交通标志中,不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
12.下列说法:①两条对角线相等的四边形是矩形;②有一组对边相等,一组对角是直角的四边形是矩形;③有一个角为直角,两条对角线相等的四边形是矩形;④四个角都相等的四边形是矩形⑤相邻两边都互相垂直的四边形是矩形.其中判断正确的个数是( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
13.将x=$\frac{2}{3}$代入反比例函数y=-$\frac{1}{x}$中,所得函数值记为y1,又将x=y1+1代入原反比例函数中,所得函数值记为y2,再将x=y2+1代入原反比例函数中,所得函数值记为y2,…,如此继续下去,则y2013=( )
| A. | -$\frac{3}{2}$ | B. | 2 | C. | -$\frac{1}{3}$ | D. | -$\frac{3}{4}$ |
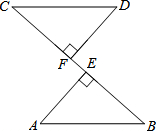 如图,DF=AE,AE⊥BC,DF⊥BC,CE=BF.求证:AB=CD.
如图,DF=AE,AE⊥BC,DF⊥BC,CE=BF.求证:AB=CD. 如图,在矩形ABCD中,已知AB=6cm,BC=8cm.将矩形ABCD绕着点D在桌面上顺时针旋转至A1B1C1D,使其停靠在矩形EFGH的点E处,若∠EDF=30°,则点B的运动路径长为$\frac{10}{3}$πcm.(结果保留π)
如图,在矩形ABCD中,已知AB=6cm,BC=8cm.将矩形ABCD绕着点D在桌面上顺时针旋转至A1B1C1D,使其停靠在矩形EFGH的点E处,若∠EDF=30°,则点B的运动路径长为$\frac{10}{3}$πcm.(结果保留π)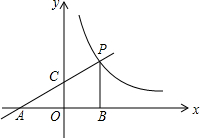 如图,一次函数y=$\frac{1}{2}$x+2的图象交x轴于点A,交y轴于点C,与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点P,C为AP的中点,PB⊥x轴于点B
如图,一次函数y=$\frac{1}{2}$x+2的图象交x轴于点A,交y轴于点C,与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点P,C为AP的中点,PB⊥x轴于点B