题目内容
18.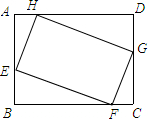 如图,矩形ABCD中,AB=3,BC=4,E、F、G、H分别在四边上,且四边形EFGH为矩形,若EF=2EH,则AE=$\frac{5}{3}$.
如图,矩形ABCD中,AB=3,BC=4,E、F、G、H分别在四边上,且四边形EFGH为矩形,若EF=2EH,则AE=$\frac{5}{3}$.
分析 根据四边形ABCD是矩形,四边形EFGH是矩形得到∠A=∠B=∠C=90°,∠HEF=90°,HE=GF,证得△AEH≌△CGF,于是得到CF=AH,由于△AEH∽△BEF,得到比例式$\frac{AH}{BE}=\frac{AE}{BF}=\frac{EH}{EF}=\frac{1}{2}$,得到BF=2AE,CF=AH=$\frac{1}{2}$BE,解方程组即可得到结论.
解答 解:∵四边形ABCD是矩形,
∴∠A=∠B=∠C=90°,
∵四边形EFGH是矩形,
∴∠HEF=90°,HE=GF,
∴∠AEH+∠BEF=∠BEF+∠BFE=90°,
∴∠AEH=∠BFE,
同理∠AEH=∠FGC,
在△AEH与△CGF中,
$\left\{\begin{array}{l}{∠A=∠C=90°}\\{∠AEH=∠CGF}\\{EH=GF}\end{array}\right.$,
∴△AEH≌△CGF,
∴CF=AH,
∵∠AEH=∠BFE,∠A=∠B,
∴△AEH∽△BEF,
∴$\frac{AH}{BE}=\frac{AE}{BF}=\frac{EH}{EF}=\frac{1}{2}$,
∴BF=2AE,CF=AH=$\frac{1}{2}$BE,
∴2AE+$\frac{1}{2}$BE=BF+CF=4,
∵AE+BE=3,
∴AE=$\frac{5}{3}$.
故答案为:$\frac{5}{3}$.
点评 本题考查了相似三角形的判定和性质,全等三角形的判定和性质,矩形的性质,熟练掌握各定理是解题的关键.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
9. M、N、P、Q四点在数轴上对应的位置和数如图所示,则它们表示的数最小的点是( )
M、N、P、Q四点在数轴上对应的位置和数如图所示,则它们表示的数最小的点是( )
 M、N、P、Q四点在数轴上对应的位置和数如图所示,则它们表示的数最小的点是( )
M、N、P、Q四点在数轴上对应的位置和数如图所示,则它们表示的数最小的点是( )| A. | 点P | B. | 点Q | C. | 点M | D. | 点 N |
13.将x=$\frac{2}{3}$代入反比例函数y=-$\frac{1}{x}$中,所得函数值记为y1,又将x=y1+1代入原反比例函数中,所得函数值记为y2,再将x=y2+1代入原反比例函数中,所得函数值记为y2,…,如此继续下去,则y2013=( )
| A. | -$\frac{3}{2}$ | B. | 2 | C. | -$\frac{1}{3}$ | D. | -$\frac{3}{4}$ |
3.孔晓东同学在“低碳大武汉,绿色在未来”演讲比赛中,6位评委给他的打分如下表:
则他得分的中位数为90.
| 评委代号 | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ | Ⅵ |
| 评 分 | 85 | 90 | 80 | 95 | 90 | 90 |
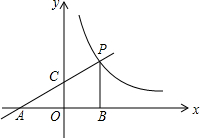 如图,一次函数y=$\frac{1}{2}$x+2的图象交x轴于点A,交y轴于点C,与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点P,C为AP的中点,PB⊥x轴于点B
如图,一次函数y=$\frac{1}{2}$x+2的图象交x轴于点A,交y轴于点C,与反比例函数y=$\frac{m}{x}$(x>0)的图象交于点P,C为AP的中点,PB⊥x轴于点B