题目内容
16. 如图,?ABCD中,两个全等的等腰直角三角形的面积都为S1,两个全等的直角三角形的面积均为S2,中间的是面积为S3正方形.求证:2S2+S3=2S1.
如图,?ABCD中,两个全等的等腰直角三角形的面积都为S1,两个全等的直角三角形的面积均为S2,中间的是面积为S3正方形.求证:2S2+S3=2S1.
分析 设等腰直角三角形的直角边为a,正方形边长为c,再求出S1,S2,S3(用a、c表示),进而得出S1,S2,S3之间的关系.
解答  证明:设等腰直角三角形的直角边为a,正方形边长为c,则
证明:设等腰直角三角形的直角边为a,正方形边长为c,则
S1=$\frac{1}{2}$a2,
S3=c2,
S2=$\frac{1}{2}$(a+c)(a-c)=$\frac{1}{2}$a2-$\frac{1}{2}$c2,
∴S2=S1-$\frac{1}{2}$S3,
∴2S2+S3=2S1.
点评 本题考查平行四边形的性质、全等三角形的性质以及正方形的性质的综合应用,解题的关键是根据S2=$\frac{1}{2}$(a+c)(a-c),求出S1,S2,S3之间的关系.

练习册系列答案
相关题目
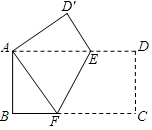 如图,把一张长为8cm,宽为4cm 的长方形纸片折叠,折叠后使相对的两个点A、C重合,点D落在D′,折痕为EF.
如图,把一张长为8cm,宽为4cm 的长方形纸片折叠,折叠后使相对的两个点A、C重合,点D落在D′,折痕为EF. 已知,在平行四边形ABCD中,E在DC上,若DE:EC=1:2,求BF:EF的值.
已知,在平行四边形ABCD中,E在DC上,若DE:EC=1:2,求BF:EF的值. 如图,点A,B,C在⊙O上,∠CAO=37°,∠CBO=33°,求∠AOB的度数.
如图,点A,B,C在⊙O上,∠CAO=37°,∠CBO=33°,求∠AOB的度数. 如图,△ABC角平分线CD交AB于点D,BC∥DE,∠ADC=95°,∠B=70°,求∠AED.
如图,△ABC角平分线CD交AB于点D,BC∥DE,∠ADC=95°,∠B=70°,求∠AED.