题目内容
6.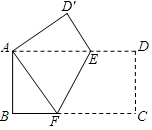 如图,把一张长为8cm,宽为4cm 的长方形纸片折叠,折叠后使相对的两个点A、C重合,点D落在D′,折痕为EF.
如图,把一张长为8cm,宽为4cm 的长方形纸片折叠,折叠后使相对的两个点A、C重合,点D落在D′,折痕为EF.(1)试说明△AEF是等腰三角形;
(2)求重合部分的面积.
分析 (1)由矩形的性质得出AD∥BC,由平行线的性质得出∠AEF=∠CFE,由折叠的性质得出∠AFE=∠CFE,AF=CF,求出∠AEF=∠AFE,得出AE=AF即可;
(2)设AE=AF=CF=x,则BF=BC-CF=8-x,在Rt△ABF中,由勾股定理得出方程,解方程求出AE=5cm,求出△AEF的面积即可.
解答 (1)证明:∵四边形ABCD是矩形,
∴AD∥BC,∠B=90°,
∴∠AEF=∠CFE,
由折叠的性质得:∠AFE=∠CFE,AF=CF,
∴∠AEF=∠AFE,
∴AE=AF,
即△AEF是等腰三角形;
(2)解:∵AE=AF,AF=CF,
∴AE=AF=CF,
设AE=AF=CF=x,则BF=BC-CF=8-x,
在Rt△ABF中,由勾股定理得:AB2+BF2=AF2,
即42+(8-x)2=x2,
解得:x=5,
∴AE=5cm,
∴△AEF的面积=$\frac{1}{2}$×5×4=10(cm2),
即重合部分的面积为10cm2.
点评 本题考查了矩形的性质、折叠的性质、等腰三角形的判定、勾股定理以及三角形面积的计算;熟练掌握矩形的性质和折叠的性质,由勾股定理得出方程是解决问题(2)的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.在一个不透明的袋中装着3个红球和1个黄球,它们只有颜色上的区别,随机从袋中摸出两个小球,两球恰好是一个黄球和一个红球的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
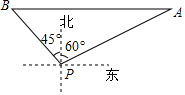 如图,一艘轮船位于灯塔P北偏东60°方向上,距离灯塔40海里的A处,它向西航行多少海里到达灯塔P北偏西45°方向上的B处.(参考数据:$\sqrt{3}$≈1.732,结果精确到0.1)
如图,一艘轮船位于灯塔P北偏东60°方向上,距离灯塔40海里的A处,它向西航行多少海里到达灯塔P北偏西45°方向上的B处.(参考数据:$\sqrt{3}$≈1.732,结果精确到0.1)
 如图,?ABCD中,两个全等的等腰直角三角形的面积都为S1,两个全等的直角三角形的面积均为S2,中间的是面积为S3正方形.求证:2S2+S3=2S1.
如图,?ABCD中,两个全等的等腰直角三角形的面积都为S1,两个全等的直角三角形的面积均为S2,中间的是面积为S3正方形.求证:2S2+S3=2S1.