题目内容
1. 如图,点A,B,C在⊙O上,∠CAO=37°,∠CBO=33°,求∠AOB的度数.
如图,点A,B,C在⊙O上,∠CAO=37°,∠CBO=33°,求∠AOB的度数.
分析 连接CO,并延长CO至点D,根据三角形外角的性质可分别表示出∠AOD,∠BOD,从图可知∠AOB等于∠AOD与∠BOD之和,再利用圆周角定理解答即可.
解答 解:连接CO,并延长CO至点D,
∵∠AOB=∠AOD+∠BOD,∠AOD=∠ACO+∠CAO,∠BOD=∠BCO+∠CBO
∴∠AOB=∠ACO+∠CAO+∠BCO+∠CBO=(∠CAO+∠CBO)+∠CBO+∠ACB=∠CAO+∠CBO+∠ACB,
∵∠AOB=2∠ACB,
可得:∠ACB+37°+33°=2∠ACB,
解得:∠ACB=70°,
所以∠AOB=140°.
点评 此题主要考查了圆周角定理的应用,要熟练掌握,解答此题的关键是要明确:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.

练习册系列答案
相关题目
11.用配方法解一元二次方程x2-6x-6=0,下列变形正确的是( )
| A. | (x-6)2=6 | B. | (x-3)2=6 | C. | (x-3)2=15 | D. | (x-6)2=42 |
 如图,将长方形纸片ABCD沿EF折叠后,点C,D分别落在点C′,D′处,若∠AFE=68°,则∠C′EF=68°.
如图,将长方形纸片ABCD沿EF折叠后,点C,D分别落在点C′,D′处,若∠AFE=68°,则∠C′EF=68°. 如图,?ABCD中,两个全等的等腰直角三角形的面积都为S1,两个全等的直角三角形的面积均为S2,中间的是面积为S3正方形.求证:2S2+S3=2S1.
如图,?ABCD中,两个全等的等腰直角三角形的面积都为S1,两个全等的直角三角形的面积均为S2,中间的是面积为S3正方形.求证:2S2+S3=2S1.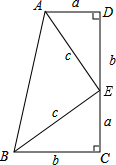 如图,已知∠C=∠D=90°,D,E,C三点共线,各边长如图所示,请利用面积法证明勾股定理.
如图,已知∠C=∠D=90°,D,E,C三点共线,各边长如图所示,请利用面积法证明勾股定理.