题目内容
如图,在图a、图b、图c中都有直线m∥n,

(1)在图a中,∠2和∠1、∠3之间的数量关系是 .
(2)猜想:在图b中,∠1、∠2、∠3、∠4之间的数量关系是 .
(3)猜想:在图c中,∠2、∠4和∠1、∠3、∠5的数量关系式是 .

(1)在图a中,∠2和∠1、∠3之间的数量关系是
(2)猜想:在图b中,∠1、∠2、∠3、∠4之间的数量关系是
(3)猜想:在图c中,∠2、∠4和∠1、∠3、∠5的数量关系式是
考点:平行线的性质
专题:规律型
分析:(1)过∠2的顶点作m∥a,根据平行公理可得a∥n,再根据两直线平行,内错角相等可得∠4=∠1,∠5=∠3,然后根据∠2=∠4+∠5计算即可得解;
(2)(3)根据顶点在左侧的角的度数之和等于顶点在右侧的角的度数之和解答.
(2)(3)根据顶点在左侧的角的度数之和等于顶点在右侧的角的度数之和解答.
解答: 解:(1)如图,过∠2的顶点作m∥a,
解:(1)如图,过∠2的顶点作m∥a,
∵m∥n,
∴a∥m∥n,
∴∠4=∠1,∠5=∠3,
∵∠2=∠4+∠5,
∴∠2=∠1+∠3;
(2)猜想:∠2+∠4=∠1+∠3;
(3)∠2+∠4=∠1+∠3+180°-∠5.
故答案为:∠2=∠1+∠3;∠2+∠4=∠1+∠3;∠2+∠4=∠1+∠3+180°-∠5.
 解:(1)如图,过∠2的顶点作m∥a,
解:(1)如图,过∠2的顶点作m∥a,∵m∥n,
∴a∥m∥n,
∴∠4=∠1,∠5=∠3,
∵∠2=∠4+∠5,
∴∠2=∠1+∠3;
(2)猜想:∠2+∠4=∠1+∠3;
(3)∠2+∠4=∠1+∠3+180°-∠5.
故答案为:∠2=∠1+∠3;∠2+∠4=∠1+∠3;∠2+∠4=∠1+∠3+180°-∠5.
点评:本题考查了平行线的性质,此类题目,过拐点作平行线是解题的关键.

练习册系列答案
相关题目
 如图,已知⊙O的直径AB=16,点C是⊙O的一点,且
如图,已知⊙O的直径AB=16,点C是⊙O的一点,且
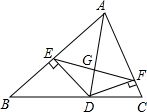 已知:如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,F,EF交AD于点G.
已知:如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,F,EF交AD于点G.
 如图,在?ABCD中,O是对角线AC和BD的交点,OE⊥AD于E,OF⊥BC于F,求证:OE=OF.
如图,在?ABCD中,O是对角线AC和BD的交点,OE⊥AD于E,OF⊥BC于F,求证:OE=OF.