题目内容
如图，已知⊙O的直径AB=16，点C是⊙O的一点，且 |
| AC |
|
| BC |
（1）求AC的长；
（2）若AD是⊙O的切线，点D与C在直径AB的两侧．
①求△CDO的面积；
②求由
|
| BC |
|
| AC |
考点：切线的性质,扇形面积的计算
专题：计算题
分析：（1）根据圆周角定理由AB为⊙O的直径得∠ACB=90°，再由
=
得AC=BC，于是可判断△ABC为等腰直角三角形，然后根据等腰直角三角形的性质得AC=
AB=8
；
（2）①根据切线的性质得AD⊥AB，再根据等腰直角三角形的性质得OC⊥CD，所以AD∥OC，则根据三角形面积公式得S△CDO=S△AOC=
•OC•AO=32；
②设由
、CD、DB围成的图形面积为S1，由
、CD、DA围成的图形面积S2，则S1=S扇形BOC+S△COD+S△BOD，S2=S扇形AOC+S△AOD-S△COD，
由于S扇形AOC=S扇形BOC，S△BOD=S△AOD，所以S1-S2=2S△COD=64．
|
| AC |
|
| BC |
| ||
| 2 |
| 2 |
（2）①根据切线的性质得AD⊥AB，再根据等腰直角三角形的性质得OC⊥CD，所以AD∥OC，则根据三角形面积公式得S△CDO=S△AOC=
| 1 |
| 2 |
②设由
|
| BC |
|
| AC |
由于S扇形AOC=S扇形BOC，S△BOD=S△AOD，所以S1-S2=2S△COD=64．
解答：解：（1）∵AB为⊙O的直径，
∴∠ACB=90°，
∵
=
，
∴AC=BC，
∴△ABC为等腰直角三角形，
∴AC=
AB=
×16=8
；
（2）①∵AD是⊙O的切线，
∴AD⊥AB，
∵OC为等腰直角三角形ABC斜边上的中线，
∴OC⊥CD，
∴AD∥OC，
∴S△CDO=S△AOC=
•OC•AO=
×8×8=32；
②设由
、CD、DB围成的图形面积为S1，由
、CD、DA围成的图形面积S2，
S1=S扇形BOC+S△COD+S△BOD，S2=S扇形AOC+S△AOD-S△COD，
∵∠AOB=∠BOC=90°，
∴S扇形AOC=S扇形BOC，
∵OA=OB，
∴S△BOD=S△AOD，
∴S1-S2=2S△COD=2×32=64，
即由
、CD、DB围成的图形面积比由
、CD、DA围成的图形面积大64．
∴∠ACB=90°，
∵
|
| AC |
|
| BC |
∴AC=BC，
∴△ABC为等腰直角三角形，
∴AC=
| ||
| 2 |
| ||
| 2 |
| 2 |
（2）①∵AD是⊙O的切线，
∴AD⊥AB，
∵OC为等腰直角三角形ABC斜边上的中线，
∴OC⊥CD，
∴AD∥OC，
∴S△CDO=S△AOC=
| 1 |
| 2 |
| 1 |
| 2 |
②设由
|
| BC |
|
| AC |
S1=S扇形BOC+S△COD+S△BOD，S2=S扇形AOC+S△AOD-S△COD，
∵∠AOB=∠BOC=90°，
∴S扇形AOC=S扇形BOC，
∵OA=OB，
∴S△BOD=S△AOD，
∴S1-S2=2S△COD=2×32=64，
即由
|
| BC |
|
| AC |
点评：本题考查了切线的性质：圆的切线垂直于经过切点的半径．也考查了圆周角定理、扇形的面积公式和三角形的面积公式．
练习册系列答案
相关题目
关于x的方程：x+
=c+
的解是x1=c，x2=
，x-
=c-
解是x1=c，x2=-
，则x+
=c+
的解是（ ）
| 1 |
| x |
| 1 |
| c |
| 1 |
| c |
| 1 |
| x |
| 1 |
| c |
| 1 |
| c |
| 1 |
| x-1 |
| 1 |
| c-1 |
A、x1=c，x2=
| ||
B、x1=c-1，x2=
| ||
C、x1=c，x2=
| ||
D、x1=c，x2=
|
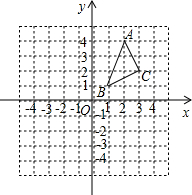△ABC在平面直角坐标系中的位置如图．A、B、C三点在格点上．
如图，△ACE是以?ABCD的对角线AC为边的等边三角形，点C与点E关于x轴对称．若E点的坐标是（7，-3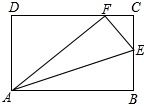
如图，矩形ABCD中，E是BC上一点，将矩形沿AE翻折后，点B恰好与CD边上的点F重合．已知AB=5，AD=3．