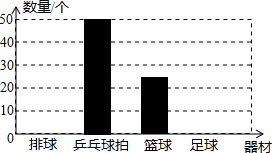
题目内容
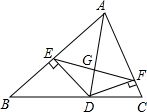 已知:如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,F,EF交AD于点G.
已知:如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E,F,EF交AD于点G.(1)判断AD与EF的位置关系,并加以说明理由.
(2)若AE=
| 5 |
考点:勾股定理,角平分线的性质
专题:
分析:(1)证得点A、D在线段EF的垂直平分线上;
(2)根据勾股定理得到AD=3,由面积法求得EG=
,从而求得EF=
.
(2)根据勾股定理得到AD=3,由面积法求得EG=
2
| ||
| 3 |
4
| ||
| 3 |
解答:(1)解:AD⊥EF.理由如下:
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF.
∴D在线段EF的垂直平分线上.
∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°,
在Rt△ADE和Rt△ADF中,
,
∴Rt△ADE≌Rt△ADF(HL).
∴AE=AF.
又∵∠EAD=∠FAD,AG=AG,
∴△AEG≌△AFG,
∴EG=GF,∠AGE=∠AGF=90°,
∴AD是线段EF的垂直平分线.
∴EF⊥AD;
(2)在直角△AED中,根据勾股定理,得
AD=3.
∵
AE•DE=
AD•EG,
∴EG=
,
∴EF=2EG=
.
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF.
∴D在线段EF的垂直平分线上.
∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°,
在Rt△ADE和Rt△ADF中,
|
∴Rt△ADE≌Rt△ADF(HL).
∴AE=AF.
又∵∠EAD=∠FAD,AG=AG,
∴△AEG≌△AFG,
∴EG=GF,∠AGE=∠AGF=90°,
∴AD是线段EF的垂直平分线.
∴EF⊥AD;
(2)在直角△AED中,根据勾股定理,得
AD=3.
∵
| 1 |
| 2 |
| 1 |
| 2 |
∴EG=
2
| ||
| 3 |
∴EF=2EG=
4
| ||
| 3 |
点评:本题考查了勾股定理,角平分线的性质.找到Rt△AED和Rt△ADF,通过两个三角形全等,找到各量之间的关系,即可证明.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
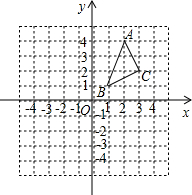 △ABC在平面直角坐标系中的位置如图.A、B、C三点在格点上.
△ABC在平面直角坐标系中的位置如图.A、B、C三点在格点上.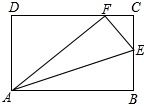 如图,矩形ABCD中,E是BC上一点,将矩形沿AE翻折后,点B恰好与CD边上的点F重合.已知AB=5,AD=3.
如图,矩形ABCD中,E是BC上一点,将矩形沿AE翻折后,点B恰好与CD边上的点F重合.已知AB=5,AD=3.