题目内容
计算
(1)(-1)2004+(-
)-2-(3.14-π)0;
(2)(2a+3b)(2a-3b)+(a-3b)2;
(3)(-2x2y+6x3y4-8xy)÷(-2xy);
(4)20052-2007×2003.
(1)(-1)2004+(-
| 1 |
| 2 |
(2)(2a+3b)(2a-3b)+(a-3b)2;
(3)(-2x2y+6x3y4-8xy)÷(-2xy);
(4)20052-2007×2003.
考点:整式的混合运算,零指数幂,负整数指数幂
专题:计算题
分析:(1)原式第一项利用乘方的意义化简,第二项利用负指数幂法则计算,第三项利用零指数幂法则计算即可得到结果;
(2)原式第一项利用平方差公式化简,第二项利用完全平方公式展开,去括号合并即可得到结果;
(3)原式利用多项式除以单项式法则计算即可得到结果;
(4)原式变形后,利用平方差公式计算即可得到结果.
(2)原式第一项利用平方差公式化简,第二项利用完全平方公式展开,去括号合并即可得到结果;
(3)原式利用多项式除以单项式法则计算即可得到结果;
(4)原式变形后,利用平方差公式计算即可得到结果.
解答:解:(1)原式=1+4-1=4;
(2)原式=4a2-9b2+a2-6ab+9b2=5a2-6ab;
(3)原式=x-3x2y3+4;
(4)原式=20052-(2005+2)×(2005-2)=20052-20052+4=4.
(2)原式=4a2-9b2+a2-6ab+9b2=5a2-6ab;
(3)原式=x-3x2y3+4;
(4)原式=20052-(2005+2)×(2005-2)=20052-20052+4=4.
点评:此题考查了整式的混合运算,以及实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
 如图,△ACE是以?ABCD的对角线AC为边的等边三角形,点C与点E关于x轴对称.若E点的坐标是(7,-3
如图,△ACE是以?ABCD的对角线AC为边的等边三角形,点C与点E关于x轴对称.若E点的坐标是(7,-3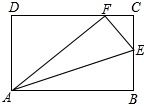 如图,矩形ABCD中,E是BC上一点,将矩形沿AE翻折后,点B恰好与CD边上的点F重合.已知AB=5,AD=3.
如图,矩形ABCD中,E是BC上一点,将矩形沿AE翻折后,点B恰好与CD边上的点F重合.已知AB=5,AD=3.