题目内容
5.在下列条件①∠A+∠B=∠C;②∠A=∠B=2∠C;③∠A=∠B=$\frac{1}{2}$∠C;④∠A﹕∠B﹕∠C=1﹕2﹕3中,能确定△ABC为直角三角形的条件有 ( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 根据三角形内角和定理和四个条件中∠A、∠B、∠C的关系,分别求出各条件下三角形中最大的角,然后根据三角形的分类进行判断.
解答 解:∵∠A+∠B+∠C=180°,
∠A+∠B=∠C,
∴∠C+∠C=180°,解得∠C=90°,
∴△ABC为直角三角形,所以①正确;
∵∠A+∠B+∠C=180°,∠A=∠B=2∠C,
∴∠A+∠A+$\frac{1}{2}$∠A=180°,
∴∠A=72°,
∴△ABC为锐角三角形,所以②错误;
∵∠A+∠B+∠C=180°,∠A=∠B=$\frac{1}{2}$∠C,
∴$\frac{1}{2}$∠C+$\frac{1}{2}$∠C+∠C=180°,
∴∠A=90°,
∴△ABC为直角三角形,所以③正确;
∵∠A:∠B:∠C=1:2:3,
设∠A=x,∠B=2x,∠C=3x,
∵∠A+∠B+∠C=180°,
∴x+2x+3x=180°,解得x=30°
∴∠C=90°,
∴△ABC为直角三角形,所以④正确.
故选B.
点评 本题考查了三角形内角和定理:三角形内角和是180°.主要用在求三角形中角的度数:①直接根据两已知角求第三个角;②依据三角形中角的关系,用代数方法求三个角;③在直角三角形中,已知一锐角可利用两锐角互余求另一锐角.也考查了直角三角形的定义.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
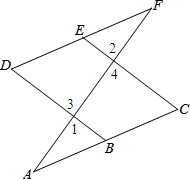 完成推理过程:如图.
完成推理过程:如图.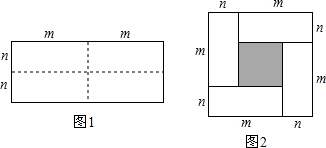
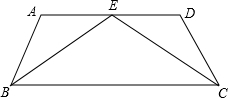 如图,AD∥BC,∠A=94°,∠D=106°,BE、CE分别是∠ABC和∠BCD的角平分线,求∠BEC的度数.
如图,AD∥BC,∠A=94°,∠D=106°,BE、CE分别是∠ABC和∠BCD的角平分线,求∠BEC的度数.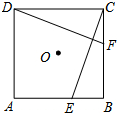 如图,E、F分别是正方形ABCD的边AB、BC上的点,BE=CF,连接CE、DF.△CDF可以看作是将△BCE绕正方形ABCD的中心O按逆时针方向旋转得到.则旋转角度为( )
如图,E、F分别是正方形ABCD的边AB、BC上的点,BE=CF,连接CE、DF.△CDF可以看作是将△BCE绕正方形ABCD的中心O按逆时针方向旋转得到.则旋转角度为( )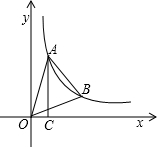 如图,点A、B在反比例函数y=$\frac{k}{x}$的图象上,且点A、B的横坐标分别为a,2a (a>0).过点A作AC⊥x轴,垂足为C,且△AOC的面积为2.
如图,点A、B在反比例函数y=$\frac{k}{x}$的图象上,且点A、B的横坐标分别为a,2a (a>0).过点A作AC⊥x轴,垂足为C,且△AOC的面积为2. 要在边长为16米的正方形草坪上安装喷水龙头,使整个草坪能喷洒到水.假设每个喷水龙头的喷洒范围都是半径为6米的圆面.则需安装这种喷水龙头的个数最少是4个.
要在边长为16米的正方形草坪上安装喷水龙头,使整个草坪能喷洒到水.假设每个喷水龙头的喷洒范围都是半径为6米的圆面.则需安装这种喷水龙头的个数最少是4个.