��Ŀ����
13��С���ܡ���ѻ��ˮ�����µ�������������Ͳ�������ͬ��С����������²������֣�����С�����Ͳ��ˮ��ĸ߶�y��cm����С�����x��������һ�κ����������ͼ�и�������Ϣ������������⣺��1����ͼ1�ɵ���Ͳ���С�����x=0ʱ����Ͳ��ԭ��ˮ��ĸ߶�y��30cm��
��ͼ1��ͼ2��������Ϣ�ɵ�����Ͳ�з����С�����x=3ʱˮ���y��36cm��
��2������Ͳ��ˮ��ĸ߶�y��cm����С�����x������֮���һ�κ�����ϵʽ����Ҫ��д���Ա�����ȡֵ��Χ����
��3����Ͳ�����ٷ��뼸��С��ʱ��ˮ�����Ϊʲô��
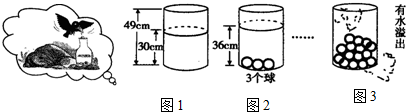
���� ��1������ͼ1����֪��Ͳ���С�����x=0ʱ����Ͳ��ԭ��ˮ��ĸ߶�y�� 30cm����ͼ1��ͼ2��������Ϣ�ɵ�����Ͳ�з����С�����x=3ʱˮ���y��36cm��
��2������������Ͱ��ˮ��ĸ߶�y��cm����С�����x������֮���һ�κ�����ϵʽΪy=kx+b���ɴ���ϵ�����Ϳ�������ۣ�
��3����y��49ʱ����������ʽ�����⼴�ɣ�
��� �⣺��1������ͼ1����֪��Ͳ���С�����x=0ʱ����Ͳ��ԭ��ˮ��ĸ߶�y��30cm��
��ͼ1��ͼ2��������Ϣ�ɵ�����Ͳ�з����С�����x=3ʱˮ���y��36cm��
�ʴ�Ϊ��30��36��
��2������������Ͱ��ˮ��ĸ߶�y��cm����С�����x������֮���һ�κ�����ϵʽΪy=kx+b�������⣬
�ã�$\left\{\begin{array}{l}{b=30}\\{3k+b=36}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=2}\\{b=30}\end{array}\right.$��
��y=2x+30��
��3����2x+30��49��
��x��9.5��
�����ٷ���10��С��ʱ��ˮ�����
���� ���⿼������һԪһ�η��̽�ʵ����������ã�����ϵ���������Ľ���ʽ�����ã��в���ʽ��ʵ����������ã����ʱ��������Ľ���ʽ�ǹؼ���

 �������Ͽ�ʱͬ��ѵ��ϵ�д�
�������Ͽ�ʱͬ��ѵ��ϵ�д� �������ͬ����ϰϵ�д�
�������ͬ����ϰϵ�д�| A�� | x=0 | B�� | -2+5=3 | C�� | $x-2=\frac{2}{x}$ | D�� | x+2y=0 |
 ��ͼ��CD��BE�����жϡ�1����2����3֮��Ĺ�ϵ����˵�����ɣ�
��ͼ��CD��BE�����жϡ�1����2����3֮��Ĺ�ϵ����˵�����ɣ� ��ͼ��AB�ǡ�O��ֱ����PB�ǡ�O�����ߣ�PA����O��C��AB=6cm��PB=8cm����BC=4.8cm��
��ͼ��AB�ǡ�O��ֱ����PB�ǡ�O�����ߣ�PA����O��C��AB=6cm��PB=8cm����BC=4.8cm��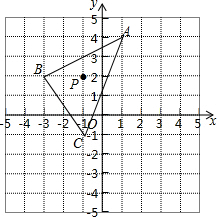 ��ͼ����ABC��������������ֱ�A��1��4����B��-3��2����C��-1��-1������P��x0��y0��Ϊ��ABC�е�����һ�㣬��ƽ�ƺ��P�Ķ�Ӧ��ΪP1��x0+3��y0-2��������ABC��ͬ����ƽ�Ƶõ���A1B1C1
��ͼ����ABC��������������ֱ�A��1��4����B��-3��2����C��-1��-1������P��x0��y0��Ϊ��ABC�е�����һ�㣬��ƽ�ƺ��P�Ķ�Ӧ��ΪP1��x0+3��y0-2��������ABC��ͬ����ƽ�Ƶõ���A1B1C1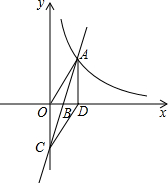 ��ͼ��ֱ��y=kx-3��k��0����x�ύ�ڵ�B����y��Ľ��ڵ�C����˫����y=$\frac{k}{x}$�ڵ�һ�����ڵĽ���Ϊ��A������A��AD��x���ڵ�D�����ı���OADC��ƽ���ı��Σ���k=3$\sqrt{2}$��
��ͼ��ֱ��y=kx-3��k��0����x�ύ�ڵ�B����y��Ľ��ڵ�C����˫����y=$\frac{k}{x}$�ڵ�һ�����ڵĽ���Ϊ��A������A��AD��x���ڵ�D�����ı���OADC��ƽ���ı��Σ���k=3$\sqrt{2}$��