题目内容
17.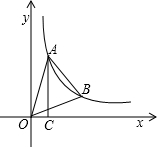 如图,点A、B在反比例函数y=$\frac{k}{x}$的图象上,且点A、B的横坐标分别为a,2a (a>0).过点A作AC⊥x轴,垂足为C,且△AOC的面积为2.
如图,点A、B在反比例函数y=$\frac{k}{x}$的图象上,且点A、B的横坐标分别为a,2a (a>0).过点A作AC⊥x轴,垂足为C,且△AOC的面积为2.(1)求该反比例函数的解析式;
(2)若a=5,设直线AB的解析式为y1=mx+b,当x满足什么条件,y<y1?
(3)求△AOB的面积.
分析 (1)根据反比例函数k的几何意义得到S△AOC=$\frac{1}{2}$|k|=2,即可得到k=4,于是得到反比例函数解析式为y=$\frac{4}{x}$;
(2)当a=5时,A(5,$\frac{4}{5}$),B(10,$\frac{2}{5}$),然后观察函数图象,找出一次函数图象在反比例函数图象上方所对应的自变量的范围即可;
(3)过点B作BD⊥x轴,垂足为D,如图,根据反比例函数图象上点的坐标特征得A(a,$\frac{4}{a}$),B(2a,$\frac{2}{a}$),由于S四边形AODB=S△AOC+S梯形ACDB=S△AOB+S△BOD,根据反比例函数k的几何意义得S△AOC=S△BOD,则S梯形ACDB=S△AOB,然后根据梯形公式计算即可.
解答 解:(1)∵AC⊥x轴,
∴S△AOC=$\frac{1}{2}$|k|,
即$\frac{1}{2}$|k|=2,
∵k>0,
∴k=4,
∴反比例函数解析式为y=$\frac{4}{x}$;
(2)当a=5时,A(5,$\frac{4}{5}$),B(10,$\frac{2}{5}$),
故当5<x<10时,y<y1;
(3)过点B作BD⊥x轴,垂足为D,如图,A(a,$\frac{4}{a}$),B(2a,$\frac{2}{a}$),
∵S四边形AODB=S△AOC+S梯形ACDB=S△AOB+S△BOD,
S△AOC=S△BOD,
∴S梯形ACDB=S△AOB,
∵S梯形ACDB=$\frac{1}{2}$•($\frac{2}{a}$+$\frac{4}{a}$)•(2a-a)=3,
∴S△AOB=3.
点评 本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.也考查了反比例函数图象上点的坐标特征.

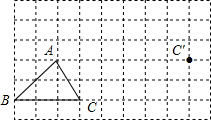 如图,△ABC平移后的图形是△A′B′C′,其中C和C′是对应点,请画出平移后的三角形A′B′C′.
如图,△ABC平移后的图形是△A′B′C′,其中C和C′是对应点,请画出平移后的三角形A′B′C′.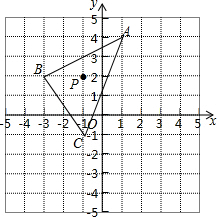 如图,△ABC的三个顶点坐标分别A(1,4),B(-3,2),C(-1,-1),点P(x0,y0)为△ABC中的任意一点,经平移后点P的对应点为P1(x0+3,y0-2),将△ABC作同样的平移得到△A1B1C1
如图,△ABC的三个顶点坐标分别A(1,4),B(-3,2),C(-1,-1),点P(x0,y0)为△ABC中的任意一点,经平移后点P的对应点为P1(x0+3,y0-2),将△ABC作同样的平移得到△A1B1C1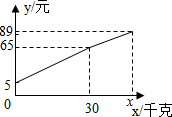 一位农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用.他将土豆按市场价售出一些后,又降价出售.售出土豆的质量x(千克)与他手中持有的钱数y(元)(含备用零钱)的函数关系如图所示.结合图象回答下列问题:
一位农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用.他将土豆按市场价售出一些后,又降价出售.售出土豆的质量x(千克)与他手中持有的钱数y(元)(含备用零钱)的函数关系如图所示.结合图象回答下列问题: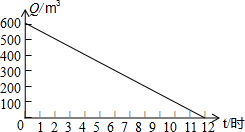 河道的剩水量Q(米3)和水泵抽水时间t(时)的关系图象如图,则水泵抽水前,河道内有600米3的水,水泵最多抽12小时,水泵抽8小时后,河道剩水量是200米3.
河道的剩水量Q(米3)和水泵抽水时间t(时)的关系图象如图,则水泵抽水前,河道内有600米3的水,水泵最多抽12小时,水泵抽8小时后,河道剩水量是200米3.