题目内容
16.乘法公式的探究及应用.图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形.
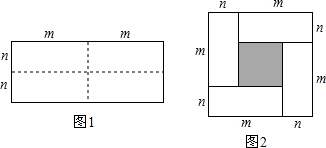
(1)请用两种不同的方法求图2中阴影部分的面积.
方法1:(m-n)2
方法2:(m+n)2-4mn
(2)观察图2请你写出下列三个代数式:(a+b)2,(a-b)2,ab之间的等量关系.
(a-b)2=(a+b)2-4ab;
(3)根据(2)题中的等量关系,解决如下问题:
①已知:a-b=5,ab=-6,求:a2+b2=13
②(a+b)2=49
②已知$x+\frac{1}{x}=3,则{x^4}+\frac{1}{x^4}$的值.
分析 (1)方法一、求出正方形的边长,再根据正方形面积公式求出即可;
方法二、根据大正方形面积减去4个矩形面积,即可得出答案;
(2)根据(1)阴影部分的面积相等,即可得出等式;
(3)①把a-b=5两边平方,利用完全平分公式,即可解答;
②根据(a+b)2=(a-b)2+4ab,即可解答;
③利用完全平分公式,即可解答.
解答 解:(1)阴影部分是正方形,正方形的边长是m-n,即阴影部分的面积是(m-n)2,
又∵阴影部分的面积S=(m+n)2-4mn,
故答案为:(m-n)2,(m+n)2-4mn.
(2)(a-b)2=(a+b)2-4ab,
故答案为:(a-b)2=(a+b)2-4ab.
(3)①∵a-b=5,ab=-6,
∴(a-b)2=52
∴a2-2ab+b2=25,
a2+b2=25+2ab=25-12=13,
故答案为:13.
②(a+b)2=(a-b)2+4ab=52-4×(-6)=49.
故答案为:49.
③${x}^{4}+\frac{1}{{x}^{4}}$
=$({x}^{2}+\frac{1}{{x}^{2}})^{2}-2$
=$[(x+\frac{1}{x})^{2}-2]^{2}-2$
=(32-2)2-2
=47.
点评 本题主要考查完全平分公式,如何准确地确定三个代数式之间的等量关系是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6. 如图,直线m、n相交,则∠1与∠2的位置关系为( )
如图,直线m、n相交,则∠1与∠2的位置关系为( )
 如图,直线m、n相交,则∠1与∠2的位置关系为( )
如图,直线m、n相交,则∠1与∠2的位置关系为( )| A. | 邻补角 | B. | 同位角 | C. | 对顶角 | D. | 内错角 |
4.下列方程是一元一次方程的是( )
| A. | x=0 | B. | -2+5=3 | C. | $x-2=\frac{2}{x}$ | D. | x+2y=0 |
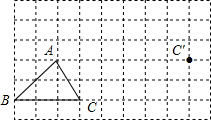 如图,△ABC平移后的图形是△A′B′C′,其中C和C′是对应点,请画出平移后的三角形A′B′C′.
如图,△ABC平移后的图形是△A′B′C′,其中C和C′是对应点,请画出平移后的三角形A′B′C′. 如图,AB是⊙O的直径,PB是⊙O的切线,PA交⊙O于C,AB=6cm,PB=8cm,则BC=4.8cm.
如图,AB是⊙O的直径,PB是⊙O的切线,PA交⊙O于C,AB=6cm,PB=8cm,则BC=4.8cm.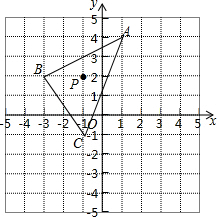 如图,△ABC的三个顶点坐标分别A(1,4),B(-3,2),C(-1,-1),点P(x0,y0)为△ABC中的任意一点,经平移后点P的对应点为P1(x0+3,y0-2),将△ABC作同样的平移得到△A1B1C1
如图,△ABC的三个顶点坐标分别A(1,4),B(-3,2),C(-1,-1),点P(x0,y0)为△ABC中的任意一点,经平移后点P的对应点为P1(x0+3,y0-2),将△ABC作同样的平移得到△A1B1C1