题目内容
15．设函数y=x+5与y=$\frac{3}{x}$的图象的两个交点的横坐标为a、b，则$\frac{1}{a}+\frac{1}{b}$的值是$\frac{5}{3}$．分析 图象的两个交点的横坐标为a、b，则a、b是方程x+5=$\frac{3}{x}$的解，把方程化成一元二次方程，利用根与系数的关系求解即可．
解答 解：根据题意得x+5=$\frac{3}{x}$，
则x2+5x-3=0，
则a+b=-5，ab=-3，
则$\frac{1}{a}+\frac{1}{b}$=$\frac{a+b}{ab}$=$\frac{-5}{-3}$=$\frac{5}{3}$．
故答案是：$\frac{5}{3}$．
点评 本题考查了反比例函数与一次函数的交点以及一元二次方程根与系数的关系，理解a、b是方程x+5=$\frac{3}{x}$的解是关键．
练习册系列答案
相关题目
5．在下列条件①∠A+∠B=∠C；②∠A=∠B=2∠C；③∠A=∠B=$\frac{1}{2}$∠C；④∠A﹕∠B﹕∠C=1﹕2﹕3中，能确定△ABC为直角三角形的条件有 （ ）
| A． | 2个 | B． | 3个 | C． | 4个 | D． | 5个 |
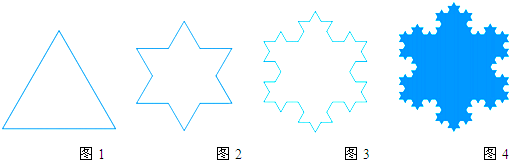
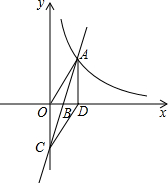如图，直线y=kx-3（k＞0）与x轴交于点B，与y轴的交于点C，与双曲线y=$\frac{k}{x}$在第一象限内的交点为点A，过点A作AD⊥x轴于点D，若四边形OADC是平行四边形，则k=3$\sqrt{2}$．
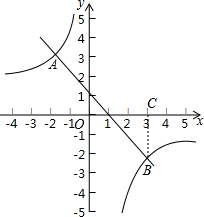如图，在平面直角坐标系xOy中，一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于点A（-2，3），B（3，n）两点．
4．a2的算术平方根一定是（ ）
| A． | a | B． | |a| | C． | $\sqrt{a}$ | D． | -a |