Question

10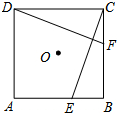．如图，E、F分别是正方形ABCD的边AB、BC上的点，BE=CF，连接CE、DF．△CDF可以看作是将△BCE绕正方形ABCD的中心O按逆时针方向旋转得到．则旋转角度为（　　）

• A． 45°
• B． 60°
• C． 90°
• D． 120°

Answer 1

分析 据旋转性质得出旋转后C到D，只要根据正方形的性质和三角形的内角和定理求出∠COD即可．

解答 解：将△CBE绕正方形的对角线交点O按逆时针方向旋转到△CDF时，C和D重合，
即∠COD是旋转角，
∵四边形ABCD是正方形，
∴∠OCD=∠ODC=45°，
∴∠COD=180°-45°-45°=90°，
即旋转角是90°，
故选C．

点评 本题主要考查了旋转的性质，以及正多边形的性质，正确理解正多边形的性质以及旋转角（对应点与旋转中心所连线段的夹角等于旋转角）是解题的关键．