题目内容
8.在△ABC中,D、E分别是AB、BC的中点,AF⊥DE于F,若DE=4cm,AF=3cm,则△ABC的面积为$\frac{3}{2}$cm2.分析 利用三角形中位线定理推知△ADE∽△ABC,由相似三角形的面积比等于相似比的平方来求△ABC的面积.
解答  解:∵AF⊥DE于F,若DE=4cm,AF=3cm,
解:∵AF⊥DE于F,若DE=4cm,AF=3cm,
∴S△ADE=$\frac{1}{2}$DE•AF=$\frac{1}{2}$×4×3=6(cm2).
∵D、E分别是AB、BC的中点,
∴DE是△ADE的中位线,
∴DE∥BC,DE=$\frac{1}{2}$BC,
∴△ADE∽△ABC,
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=($\frac{DE}{BC}$)2=$\frac{1}{4}$,
∴S△ABC=4S△ADE=$\frac{3}{2}$(cm2).
故答案是:$\frac{3}{2}$cm2.
点评 此题考查的是三角形中位线的性质,即三角形的中位线平行于第三边且等于第三边的一半.

练习册系列答案
相关题目
 如图,AB=AE,BC=ED,AF⊥CD,∠B=∠E.F是CD的中点吗?为什么?
如图,AB=AE,BC=ED,AF⊥CD,∠B=∠E.F是CD的中点吗?为什么?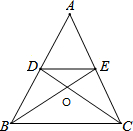 已知:如图,在△ABC中,AB=AC,BE和CD是中线.
已知:如图,在△ABC中,AB=AC,BE和CD是中线.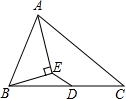 如图,AE平分∠BAC,BE⊥AE,垂足为E,D为BC的中点,∠BAE=36°,则∠BED的度数是126°.
如图,AE平分∠BAC,BE⊥AE,垂足为E,D为BC的中点,∠BAE=36°,则∠BED的度数是126°.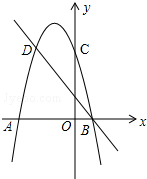 如图,二次函数的图象与x轴交于A(-3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
如图,二次函数的图象与x轴交于A(-3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.