题目内容
13.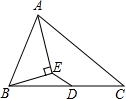 如图,AE平分∠BAC,BE⊥AE,垂足为E,D为BC的中点,∠BAE=36°,则∠BED的度数是126°.
如图,AE平分∠BAC,BE⊥AE,垂足为E,D为BC的中点,∠BAE=36°,则∠BED的度数是126°.
分析 延长BE交AC于点F,根据∠BAE=36°求出∠ABE的度数,再由AE平分∠BAC得出∠BAC的度数,根据三角形内角和定理得出∠AFE的度数,故可得出△ABF是等腰三角形,点E是BF的中点,根据D为BC的中点得出DE是△BCF的中位线,故DE∥AC,根据两直线平行同旁内角互补,可求得∠DEA的度数,再由三角形外角和为360°求得∠BED度数.
解答 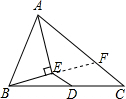 解:延长BE交AC于点F,
解:延长BE交AC于点F,
∵∠BAE=36°,BE⊥AE,
∴∠ABE=90°-36°=54°.
∵AE平分∠BAC,
∴∠BAC=2∠BAE=72°,
∴∠AFE=180°-72°-54°=54°,
∴△ABF是等腰三角形,
∴点E是BF的中点.
∵D为BC的中点,
∴DE是△BCF的中位线,
∴DE∥AC,
∴∠CAE+∠DEA=180°
∴∠DEA=180°-36°=144°
∵∠AED+∠AEB+∠BED=360°
∴∠BED=360°-144°-90°=126°.
故答案为126°.
点评 本题考查的是三角形中位线定理,涉及到平行线的性质和三角形外角和定理.两直线平行,同旁内角互补.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
5.在平面直角坐标系xOy中,第一象限内的点P在反比例函数的图象上,如果点P的纵坐标是3,OP=5,那么该函数的表达式为( )
| A. | y=$\frac{12}{x}$ | B. | y=-$\frac{12}{x}$ | C. | y=$\frac{15}{x}$ | D. | y=-$\frac{15}{x}$ |
2.一个不透明的口袋里有4张形状完全相同的卡片,分别写有数字1,2,3,4,口袋外有两张卡片,分别写有数字2,3,现随机从口袋里取出一张卡片,则两次摸出的卡片的数字之和等于4的概率( )
| A. | $\frac{3}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | 1 |
3.3-1的值等于( )
| A. | -3 | B. | 3 | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
 如图,四边形ABDE,ACFG都是正方形.求证:
如图,四边形ABDE,ACFG都是正方形.求证: