题目内容
19.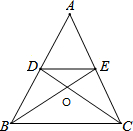 已知:如图,在△ABC中,AB=AC,BE和CD是中线.
已知:如图,在△ABC中,AB=AC,BE和CD是中线.(1)求证:BE=CD.
(2)求$\frac{OE}{OB}$的值.
分析 (1)由三角形全等得到对应边相等,证得结论;
(2)由相似三角形得到对应边的比相等,再根据三角形的中位线定理得到对应边的比等于$\frac{1}{2}$.
解答 解:(1)证明:∵AB=AC,BE和CD是中线,
∴AD=$\frac{1}{2}$AB,AE=$\frac{1}{2}$AC,
∴AD=AE,
在△ABE与△ACD中,$\left\{\begin{array}{l}{AB=AC}\\{∠A=∠A}\\{AD=AE}\end{array}\right.$,
∴△ABE≌△ACD,
∴BE=CD;
(2)∵BE和CD是中线,
∴AD=BD,AE=CE,
∴DE∥BC,DE=$\frac{1}{2}$BC,
∴△DEO∽△BCO,
∴$\frac{OE}{OB}$=$\frac{DE}{BC}$=$\frac{1}{2}$.
点评 本题考查了等腰三角形的性质,全等三角形的判定与性质,三角形的中位线定理,三角形的中线,相似三角形的判定和性质,熟记相似三角形的判定定理是关键.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
9.为了加强公民的节水意识,合理利用水资源,某市采用价格调控手段达到节水的目的,该市自来水收费价格见表,例如:某户居民1月份用水15立方米,则应收水费:2×10+3×(15-10)=35(元).
(1)若该户居民2月份用水24立方米,则应收水费多少元?
(2)若该户居民3、4月份共用水26立方米(3月份用水量不超过10立方米),共交水费60元,则该户居民3、4月份各用水多少立方米?
| 每月用水量 | 单价 |
| 不超出10立方米的部分 | 2元/立方米 |
| 超出10立方米不超出20立方米部分 | 3元/立方米 |
| 超出20立方米的部分 | 4元/立方米 |
(2)若该户居民3、4月份共用水26立方米(3月份用水量不超过10立方米),共交水费60元,则该户居民3、4月份各用水多少立方米?
9.如果点A(-4,y1),B(-1,y2),C(3,y3)都在反比例函数$y=\frac{k}{x}(k<0)$的图象上,那么y1,y2,y3的大小关系是( )
| A. | y1<y3<y2 | B. | y3<y1<y2 | C. | y1<y2<y3 | D. | y3<y2<y1 |

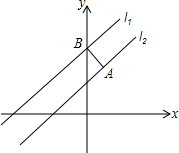 如图所示,已知两条直线l1:y=2x+7,l2:y=2x+5,在l2上任取一点A,过点A作直线l1的垂线,垂足为B点,求AB的长.
如图所示,已知两条直线l1:y=2x+7,l2:y=2x+5,在l2上任取一点A,过点A作直线l1的垂线,垂足为B点,求AB的长.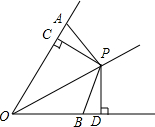 如图所示,P为∠AOB的平分线上一点,PC⊥OA于C,∠OAP+∠OBP=180°,若OC=4cm,求AO+OB的长.
如图所示,P为∠AOB的平分线上一点,PC⊥OA于C,∠OAP+∠OBP=180°,若OC=4cm,求AO+OB的长.